题目内容
已知:如图,P是△ABC内任一点,求证:AB+AC>BP+PC.
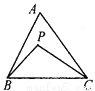
 证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC,
证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC,
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
下列图形中对称轴最多的是( )
A. 圆 B. 正方形 C. 角 D. 线段
 A
【解析】试题分析:根据轴对称图形的对称轴的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.这条直线就是它的对称轴.
【解析】
A、圆的对称轴有无数条,它的每一条直径所在的直线都是它的对称轴;
B、正方形的对称轴有4条;
C、角的对称轴有1条;
D、线段的对称轴有2条.
故图形中对称轴最多的是圆.
故选A.
...
A
【解析】试题分析:根据轴对称图形的对称轴的概念:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.这条直线就是它的对称轴.
【解析】
A、圆的对称轴有无数条,它的每一条直径所在的直线都是它的对称轴;
B、正方形的对称轴有4条;
C、角的对称轴有1条;
D、线段的对称轴有2条.
故图形中对称轴最多的是圆.
故选A.
... 对于圆的周长公式C=2πR,下列说法中,正确的是( )
A. 2π是变量 B. 2πR是常量 C. C是R的函数 D. 该函数没有定义域
 C
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.R是变量,2、π是常量,C是R的函数,该函数的定义域为R>0,故选C.
C
【解析】常量就是在变化过程中不变的量,变量是指在变化过程中随时可以发生变化的量.R是变量,2、π是常量,C是R的函数,该函数的定义域为R>0,故选C. 已知点M(-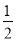 ,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
,3m)关于原点对称的点在第一象限,那么m的取值范围是____________.
 m<0
【解析】因为点M(,3m)关于原点对称的点在第一象限,所以-3m>0,所以m<0,故答案为:m<0.
m<0
【解析】因为点M(,3m)关于原点对称的点在第一象限,所以-3m>0,所以m<0,故答案为:m<0. 已知反比例函数和正比例函数在第一象限的交点为A(1,3),则在第三象限的交点B为( )
A. (-1,-3) B. (-3,-1) C. (-2,-6) D. (-6,-2)
 A
【解析】因为反比例函数是中心对称图形,正比例函数与反比例函数的图象的两个交点关于原点对称,又因为一个交点的坐标为A(1,3),所以它的另一个交点的坐标是(-1,-3),故选A.
A
【解析】因为反比例函数是中心对称图形,正比例函数与反比例函数的图象的两个交点关于原点对称,又因为一个交点的坐标为A(1,3),所以它的另一个交点的坐标是(-1,-3),故选A. 如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为11cm,求AC的长.
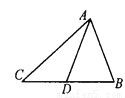
 8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm.
8cm.
【解析】试题分析:根据中线的定义知CD=BD,结合三角形的周长公式知AC﹣AB=5cm,又AB+AC=11cm,易求AC的长度.
试题解析:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长﹣△ABD的周长=5cm.
∴AC﹣AB=5cm.
又∵AB+AC=11cm,
∴AC=8cm.即AC的长度是8cm. 如图,△ABC的两个外角的平分线相交于点D,如果∠A=50°,那么∠D=_____.
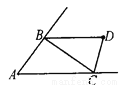
 65°
【解析】试题解析:
故答案为:
65°
【解析】试题解析:
故答案为: 在△ABC中,AB=4a,BC=14,AC=3a.则a的取值范围是 ( )
A. a>2 B. 2<a<14 C. 7<a<14 D. a<14
 B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2
B
【解析】试题解析:∵△ABC中,AB=4a,BC=14,AC=3a,
∴解得2如图,在平面直角坐标系xOy中,已知点A(2,1)和点B(3,0),则sin∠AOB的值等于( )
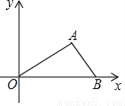
A. 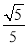 B.
B. 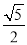 C.
C. 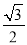 D.
D. 
 A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A
A
【解析】试题解析:过A作AC⊥x轴,
∵A(2,1),
∴AC=1,OC=2,
在Rt△AOC中,根据勾股定理得:OA=,
则sin∠AOB=,
故选A 
