题目内容
将点A(3，2)沿x轴向左平移4个单位长度得到点A′，则点A′关于原点对称的点的坐标是( )
A. (-3，2) B. (-1，2) C. (1，2) D. (1，-2)
D
【解析】试题分析：将点A（3，2）向左平移4个单位长度得点A′，可得点A′的坐标为（﹣1，2），所以点A′关于y轴对称的点的坐标是（1，2），故选D．
对于下列命题：（1）关于某一直线成轴对称的两个三角形全等；（2）等腰三角形的对称轴是顶角的平分线；（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点；（4）如果两个三角形全等，那么它们关于某直线成轴对称。其中真命题的个数为
A、0 B、1 C、2 D、3
C
【解析】
试题分析：根据平面图形的基本概念依次分析各小题即可作出判断.
（1）关于某一直线成轴对称的两个三角形全等，（3）一条线段的两个端点一定是关于经过该线段中点的直线的对称点，均为真命题；
（2）等腰三角形的对称轴是顶角的平分线所在的直线，（4）如果两个三角形全等，它们可能是平移或旋转构成的，均为假命题；
故选C. 在动画片《喜羊羊与灰太狼》中，有一次灰太狼追赶喜羊羊，在距羊村40m处追上了喜羊羊．如图中s表示它们与羊村的距离（单位：m），t表示时间（单位：s）．根据相关信息判断，下列说法中错误的是（ ）
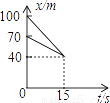
A. 喜羊羊与灰太狼最初的距离是30m B. 灰太狼用15s追上了喜羊羊
C. 灰太狼跑了60m追上了喜羊羊 D. 灰太狼追上喜羊羊时，喜羊羊跑了60m
D
【解析】观察图象可得，喜羊羊与灰太狼最初的距离是100-70=30m，选项A正确；由横坐标看出，15秒灰太狼追上了喜羊羊，选项B正确；由纵坐标看出，灰太狼跑了100-40=60米追上喜羊羊，选项C正确；由纵坐标看出，灰太狼追上喜羊羊时喜羊羊跑了70-40=30米，选项D错误；故选D． 如果点A(－3，2m+1)关于原点对称的点在第四象限，求m的取值范围.
m＞－
【解析】试题分析：由于第四象限关于原点对称的点在第二象限，反之第二象限的点关于原点对称的点在第四象限，所以A(－3,2m+1)应在第二象限，由第二象限的符号特征解之.
∵A(－3，2m+1)关于原点对称的点在第四象限.
∴A(－3，2m+1)在第二象限.
∴A点的纵坐标2m+1＞0.
∴m＞－. 点M(2，-3）与点N（2，3）关于______对称；点A(-2，-4）与点B（2，4）关于______对称；点G(4，0）与点H（-4，0）关于____________对称.
x轴 原点 y轴
【解析】根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,关于原点的对称点,横纵坐标都变成相反数,关于y轴对称的点的坐标规律:横坐标互为相反数,纵坐标相同,
所以点M与点N关于x轴对称,点A与点B关于原点对称,点G与点H关于y轴对称,故答案为: x轴, 原点, y轴. △ABC中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，求∠A的度数．
44°
【解析】试题分析：先用∠A表示出∠C，再根据三角形的内角和等于180°列式整理用
∠A表示出∠B，再根据不等式求出∠A的取值范围，最后根据∠A是整数解答．
试题解析：
∵4∠C=7∠A，
∵∠A<∠B<∠C，
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍， 如图，点B、C、D、E共线，试问图中A、B、C、D、E五点可确定多少个三角形?说明理由．
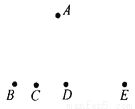
6个.
【解析】试题分析：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，因而三角形的个数就是B、C、D、E四点中，两个分成一组，点的组数．
试题解析：可以确定6个三角形.
理由：经过两点可以确定一条线段，而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形，
所以图中可以确定6个三角形. 如图，已知∠ACB=90°，CD⊥AB，垂足是D，则图中与∠A相等的角是 ( )
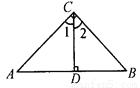
A. ∠1 B. ∠2 C. ∠B D. ∠1、∠2和∠B
B
【解析】试题解析：
∵∠ACB=即∠1+∠2=
又∵中,∠A+∠1=
∴∠A=∠2.
故选B. 如图，学校大门出口处有一自动感应栏杆，点A是栏杆转动的支点，当车辆经过时，栏杆AE会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度∠BAE＝127°，已知AB⊥BC，支架AB高1.2米，大门BC打开的宽度为2米，以下哪辆车可以通过？( )(栏杆宽度，汽车反光交镜忽略不计)(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，车辆尺寸：长×宽×高)
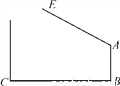
A. 宝马Z4(4200 mm×1800 mm×1360 mm) B. 奇瑞QQ(4000 mm×1600 mm×1520 mm)
C. 大众朗逸(4600 mm×1700 mm×1400 mm) D. 奥迪A4(4700 mm×1800 mm×1400 mm)
C
【解析】试题解析：如图，过点A作BC的平行线AG，过点N作NQ⊥BC于Q，交AG于点R，
则∠BAG=90°，
∵∠BAE=127°，∠BAG=90°，
∴∠EAH=∠EAB-∠BAG=37°．
在△NAR中，∠ARN=90°，∠EAG=37°，
当车宽为1.8m，则GR=1.8m，故AR=2-1.8=0.2（m），
∴NR=ARtan37°=0.2×...