题目内容
已知反比例函数和正比例函数在第一象限的交点为A(1,3),则在第三象限的交点B为( )
A. (-1,-3) B. (-3,-1) C. (-2,-6) D. (-6,-2)
 A
【解析】因为反比例函数是中心对称图形,正比例函数与反比例函数的图象的两个交点关于原点对称,又因为一个交点的坐标为A(1,3),所以它的另一个交点的坐标是(-1,-3),故选A.
A
【解析】因为反比例函数是中心对称图形,正比例函数与反比例函数的图象的两个交点关于原点对称,又因为一个交点的坐标为A(1,3),所以它的另一个交点的坐标是(-1,-3),故选A.
练习册系列答案
相关题目
下列图形中,轴对称图形有( )




A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】【解析】
给出的四个图形中,只有第一个是轴对称图形,其余虽然外形是,但是其内部图形不是,故选A.
A
【解析】【解析】
给出的四个图形中,只有第一个是轴对称图形,其余虽然外形是,但是其内部图形不是,故选A. 汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内余油量Q(升)与行驶时间t(时)的关系用图象表示应为图中的是( )
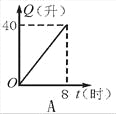
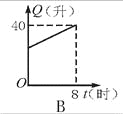
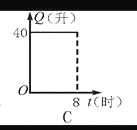
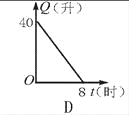
 D
【解析】油箱内有油40升,那么余油量最初应是40,排除A. B;
随着时间的增多,余油量就随之减少,排除C.
正确的为D.
故选D.
D
【解析】油箱内有油40升,那么余油量最初应是40,排除A. B;
随着时间的增多,余油量就随之减少,排除C.
正确的为D.
故选D. 求cos42°,下列按键正确的是( )
A. 

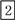
 B.
B. 


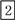

C. 


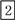 D.
D. 



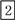
 A
【解析】试题解析:用计算器计算一个锐角的三角函数值的步骤,先三角函数,之后度数,最后等号;
故选A.
A
【解析】试题解析:用计算器计算一个锐角的三角函数值的步骤,先三角函数,之后度数,最后等号;
故选A. 直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′为________.
 P′为(-3,-6)
【解析】因为直线y=x+3上有一点P(3,n),所以n=3+3=6,所以P(3,6),所以点P关于原点的对称点P′为(-3,-6),故答案为:(-3,-6).
P′为(-3,-6)
【解析】因为直线y=x+3上有一点P(3,n),所以n=3+3=6,所以P(3,6),所以点P关于原点的对称点P′为(-3,-6),故答案为:(-3,-6). 已知:如图,P是△ABC内任一点,求证:AB+AC>BP+PC.
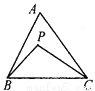
 证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC,
证明见解析.
【解析】试题分析:延长BP交AC于点D,由三角形的三边关系可得AB+AD>BD,PD+DC>PC,
试题解析:如图,延长BP交AC于点D.
在△ABD中,根据三边关系可得:
∵BD=BP+DP,
∴AB+AD>BP+DP.
在△PCD中,根据三边关系可得:PD+DC>PC, 如图,∠BAD=∠CAD,则AD是△ABC的角平分线,对吗?说明理由.
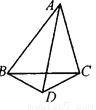
 不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分...
不是,理由见解析.
【解析】试题分析:考查了三角形的角平分线的定义,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线.
试题解析:根据三角形的角平分线的定义,可知:①平分三角形的一个内角;②是一条线段,一个端点是三角形的顶点,另一点在这个顶点的对边上.而此题中AD满足①,但点D不在BC边上,故不满足②.所以,AD不是△ABC的角平分... 点P是△ABC内任意一点,则∠APC与∠B的大小关系是 ( )
A. ∠APC>∠B B. ∠APC=∠B C. ∠APC<∠B D. 不能确定
 A
【解析】试题解析:
如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A.
A
【解析】试题解析:
如图,延长AP与BC相交于点D,
由三角形的外角性质得,∠PDC>∠B,∠APC>∠PDC,
所以,∠APC>∠B.
故选A. 在Rt△ABC中,如果各边长度都扩大为原来的2倍,那么锐角A的正弦值( )
A. 扩大2倍 B. 缩小2倍 C. 扩大4倍 D. 没有变化
 D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D.
D
【解析】根据锐角三角函数的概念,知若各边长都扩大2倍,则sinA的值不变.
故选D. 
