如图，将一副三角板叠放在一起，使直角的顶点重合于O，则∠AOC+∠DOB=（ ）
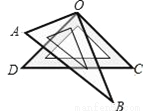
A. 90° B. 120° C. 160° D. 180°
D
【解析】设∠AOD=a,∠AOC=90°+a,∠BOD=90°?a，
所以∠AOC+∠BOD=90°+a+90°?a=180°.
故选D. 以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边，可以画出三角形的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
C
【解析】
试题解析：首先可以组合为13，10，5；13，10，7；13，5，7；10，5，7．再根据三角形的三边关系，发现其中的13，5，7不符合，则可以画出的三角形有3个．
故选C． 一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________．
37cm
【解析】①7cm是腰长时，三角形的三边分别为7cm、7cm、15cm，
∵7+7=14<15，
∴不能组成三角形，
②7cm是底边时，三角形的三边分别为7cm、15cm、15cm，
能组成三角形，
周长=7+15+15=37cm，
综上所述，它的周长是37cm.
故答案为：37cm. 如图：（1）AD⊥BC，垂足为D，则AD是__的高，∠__=∠__=90°；
（2）AE平分∠BAC，交BC于点E，则AE叫__，∠__=∠__=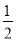
∠__，AH叫__；
（3）若AF=FC，则△ABC的中线是__；
（4）若BG=GH=HF，则AG是__的中线，AH是__的中线．
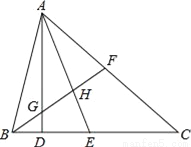
BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析：(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线；
(3)若AF=FC，则△ABC的中线是BF；
(4)若BG=GH=HF，则AG是△ABH的中线... 如图，△ABC中，∠ABC、∠ACB的平分线相交于点I．
（1）若∠ABC=70°，∠ACB=50°，则∠BIC=__；
（2）若∠ABC+∠ACB=120°，则∠BIC=__；
（3）若∠A=60°，则∠BIC=__；
（4）若∠A=100°，则∠BIC=__；
（5）若∠A=n°，则∠BIC=__．
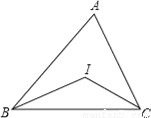
120° 120°， 120° 140°， 90°+n°．
【解析】试题解析：(1)∵BI是∠ABC的平分线，
∵CI是∠ACB的平分线，
在△BCI中，
(2)∵BI是∠ABC的平分线，CI是∠ACB的平分线，
在△BCI中，
(3)在△ABC中，
∵BI是∠ABC的平分线，CI是∠ACB的平分线，
在△BCI中，
(4)在△ABC中，
... 如图5—13，在△ABC中，AD⊥BC，GC⊥BC，CF⊥AB，BE⊥AC，垂足分别为D、C、F、E，则_______是△ABC中BC边上的高，_________是△ABC中AB边上的高，_________是 △ABC中AC边上的高，CF是△ABC的高，也是△_______、△_______、△_______、△_________的高．
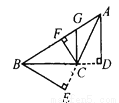
AD CF BE BFC FGC FAC GAC
【解析】试题解析：AD是△ABC中BC边上的高，是△ABC中AB边上的高，BE是△ABC中AC边上的高，CF是△ABC的高，也是△BFC、△FGC、△FAC、△GAC的高.
故答案是：AD、CF、BE、BFC、FGC、FAC、GAC. 把一副常用的三角形如图所示拼在一起，那么图中∠ADE是__度．
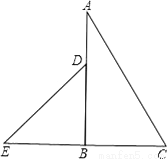
135°
【解析】试题分析：根据三角板可得：∠BDE=45°，则根据平角的性质可得：∠ADE=180°-45°=135°. 若三角形三个内角度数的比为2：3：4，则相应的外角比是__．
7：6：5
【解析】试题分析：由三角形的内角和是180°，三个内角的度数的比为2：3：4，可求得三个内角分别为40°，
60°，80°；从而对应的三个外角分别为140°，120°，100°；即可求得相应的的外角比. 如图，△ABC中，∠A=40°，∠B=72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=__度．
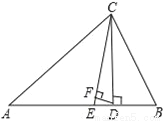
74°
【解析】试题解析：
∵CE平分∠ACB，CD⊥AB于D，
∵DF⊥CE，
故答案为：74.