题目内容
一个等腰三角形两边的长分别是15cm和7cm则它的周长是__________.
 37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm.
37cm
【解析】①7cm是腰长时,三角形的三边分别为7cm、7cm、15cm,
∵7+7=14<15,
∴不能组成三角形,
②7cm是底边时,三角形的三边分别为7cm、15cm、15cm,
能组成三角形,
周长=7+15+15=37cm,
综上所述,它的周长是37cm.
故答案为:37cm.
练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知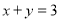 ,
, 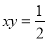 ,则多项式
,则多项式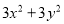 的值为( ).
的值为( ).
A. 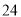 B.
B. 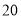 C.
C. 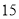 D.
D. 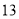
 A
【解析】试题解析:∵x+y=3,
故选A.
A
【解析】试题解析:∵x+y=3,
故选A. 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
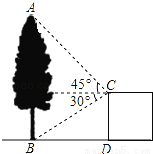
 5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m.
5+5.
【解析】
试题分析:作CE⊥AB于点E,
在Rt△BCE中,
BE=CD=5m,
CE==5m,
在Rt△ACE中,
AE=CE•tan45°=5m,
AB=BE+AE=(5+5)m. 如图,AB∥CD,BC⊥AB,若AB=4cm,S△ABC=12cm2,求△ABD中AB边上的高.
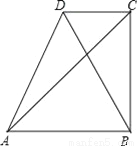
 6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm.
6cm.
【解析】试题分析:根据三角形的面积求出的边AB上的高BC,再根据平行线间的距离相等解答.
试题解析:
解得:
∵AB∥CD,
∴点D到AB边的距离等于BC的长度,
∴中AB边上的高等于6cm. 把一副常用的三角形如图所示拼在一起,那么图中∠ADE是__度.
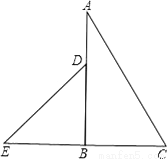
 135°
【解析】试题分析:根据三角板可得:∠BDE=45°,则根据平角的性质可得:∠ADE=180°-45°=135°.
135°
【解析】试题分析:根据三角板可得:∠BDE=45°,则根据平角的性质可得:∠ADE=180°-45°=135°. 如图,在直角三角形ABC中,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(除之C外)相等的角的个数是( )
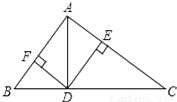
A. 2 B. 3 C. 4 D. 5
 B
【解析】试题分析:图中与∠C(除之C外)相等的角有∠ADE、∠FAD、∠FDB共3个,故答案选B.
B
【解析】试题分析:图中与∠C(除之C外)相等的角有∠ADE、∠FAD、∠FDB共3个,故答案选B. 三角形的一个外角是锐角,则此三角形的形状是( )
A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 无法确定
 B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。
B
【解析】本题主要考查了三角形的形状
根据外角是锐角,可得相邻的内角是钝角,即可判断。
一个外角是锐角,相邻的内角是钝角,这是一个钝角三角形,故选B。 如图,点B在射线AE上,△CBA沿射线AE翻折后能与⊿DBA重合,则正确的是( )
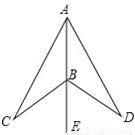
A. CA=DB B. ∠CAE=∠DBE C. AC=AD D. ∠CBA=∠DBE
 C
【解析】∵△CBA沿射线AE翻折后能与△DBA重合,
∴∠D=∠C,∠CAB=∠DAB,∠CBA=∠DBA,AC=AD,
故选C.
C
【解析】∵△CBA沿射线AE翻折后能与△DBA重合,
∴∠D=∠C,∠CAB=∠DAB,∠CBA=∠DBA,AC=AD,
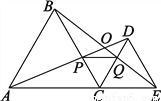
故选C. 如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是___________.
 ①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC...
①②③⑤
【解析】试题解析:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=
∴△PC... 
