��Ŀ����
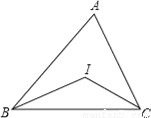
��ͼ����ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�I��
��1������ABC=70�㣬��ACB=50�㣬���BIC=__��
��2������ABC+��ACB=120�㣬���BIC=__��
��3������A=60�㣬���BIC=__��
��4������A=100�㣬���BIC=__��
��5������A=n�㣬���BIC=__��
 120�� 120�㣬 120�� 140�㣬 90��+n�㣮
�����������������(1)��BI�ǡ�ABC��ƽ���ߣ�
��CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(2)��BI�ǡ�ABC��ƽ���ߣ�CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(3)�ڡ�ABC�У�
��BI�ǡ�ABC��ƽ���ߣ�CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(4)�ڡ�ABC�У�
...
120�� 120�㣬 120�� 140�㣬 90��+n�㣮
�����������������(1)��BI�ǡ�ABC��ƽ���ߣ�
��CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(2)��BI�ǡ�ABC��ƽ���ߣ�CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(3)�ڡ�ABC�У�
��BI�ǡ�ABC��ƽ���ߣ�CI�ǡ�ACB��ƽ���ߣ�
�ڡ�BCI�У�
(4)�ڡ�ABC�У�
...
ij�ֵ���Ԫ���������ԼΪ0.00000069ƽ�����ף���0.00000069������ÿ�ѧ��������ʾΪ______��
 6.9��10��7��
�������������������ֵС��1������Ҳ�������ÿ�ѧ��������ʾ��һ����ʽΪa��10��n����ϴ����Ŀ�ѧ��������ͬ��������ʹ�õ��Ǹ�ָ���ݣ�ָ����ԭ��������һ����Ϊ�������ǰ���0�ĸ���������������0.00000069=6.9��10��7��
6.9��10��7��
�������������������ֵС��1������Ҳ�������ÿ�ѧ��������ʾ��һ����ʽΪa��10��n����ϴ����Ŀ�ѧ��������ͬ��������ʹ�õ��Ǹ�ָ���ݣ�ָ����ԭ��������һ����Ϊ�������ǰ���0�ĸ���������������0.00000069=6.9��10��7�� ��Rt��ABC�У���C=90�㣬a=8����B=60�㣬�����ֱ�������Σ�
 ��A=30�㣬AB=16��AC=
����������������������������ڽǺͶ��������A�����ݺ�30�Ƚ�ֱ�����������AB�����ݹ��ɶ������AC���ɣ�
����������ߡ�C=90�㣬��B=60�㣬
���A=180��-��C-��B=30�㣬
��BC=a=8��
��AB=2a=16��
�ɹ��ɶ����ã�AC= ��
��A=30�㣬AB=16��AC=
����������������������������ڽǺͶ��������A�����ݺ�30�Ƚ�ֱ�����������AB�����ݹ��ɶ������AC���ɣ�
����������ߡ�C=90�㣬��B=60�㣬
���A=180��-��C-��B=30�㣬
��BC=a=8��
��AB=2a=16��
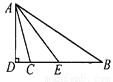
�ɹ��ɶ����ã�AC= �� ��ͼ����ABC�У���B=34�㣬��ACB=104�㣬AD��BC���ϵĸߣ�AE�ǡ�BAC��ƽ���ߣ����DAE�Ķ�����
 35��.
���������������ε��ڽǺͶ����������BAC=70�㣬����AE�ǡ�BAC��ƽ���ߣ������BAE=35�㣬����AD��BC���ϵĸߣ���֪��ADB=90�㣬�����BAD=25�㣬���ԡ�DAE=��BAE-��BAD=10�㣮
��������
�ڡ�ABC�У�
�ߡ�BAC=180��-��B-��C=70�㣬
��AE�ǡ�BAC��ƽ���ߣ�
���BAE=��CAE=35�㣮
�֡�AD��BC���ϵĸߣ�...
35��.
���������������ε��ڽǺͶ����������BAC=70�㣬����AE�ǡ�BAC��ƽ���ߣ������BAE=35�㣬����AD��BC���ϵĸߣ���֪��ADB=90�㣬�����BAD=25�㣬���ԡ�DAE=��BAE-��BAD=10�㣮
��������
�ڡ�ABC�У�
�ߡ�BAC=180��-��B-��C=70�㣬
��AE�ǡ�BAC��ƽ���ߣ�
���BAE=��CAE=35�㣮
�֡�AD��BC���ϵĸߣ�... ���������Ϊa��2��a+5��a+2�������߶���β˳����ӿ��Եõ�һ�������Σ���ôa��ȡֵ��Χ��____________
 a>5
����������Ϊ?2<2<5������a?2< a+2< a+5��
���������������߹�ϵ�ɵ�a?2+a+2>a+5�����a>5.
a>5
����������Ϊ?2<2<5������a?2< a+2< a+5��
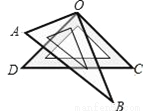
���������������߹�ϵ�ɵ�a?2+a+2>a+5�����a>5. ��ͼ����һ�����ǰ������һ��ʹֱ�ǵĶ����غ���O�����AOC+��DOB=��������
A. 90�� B. 120�� C. 160�� D. 180��
 D
�����������AOD=a,��AOC=90��+a,��BOD=90��?a��
���ԡ�AOC+��BOD=90��+a+90��?a=180��.
��ѡD.
D
�����������AOD=a,��AOC=90��+a,��BOD=90��?a��
���ԡ�AOC+��BOD=90��+a+90��?a=180��.
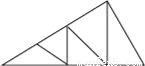
��ѡD. ͼ�������εĸ����ǣ�������
A. 8�� B. 9�� C. 10�� D. 11��
 B
�������������������ͼ�е��������У���AGD����ADF����AEF����AEC����ABC����DGF����DEF����CEF����CEB��
�9��������.
��ѡB.
B
�������������������ͼ�е��������У���AGD����ADF����AEF����AEC����ABC����DGF����DEF����CEF����CEB��
�9��������.
��ѡB. ��ͼ��ABC��ʹA��D�غϣ����ABC______��DBC�����Ӧ��Ϊ_____����Ӧ����_______.
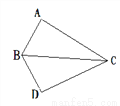
 �� ��A=��D����ABC=��DBC����ACB=��DCB AB��DB��AC��DC��BC��BC.
�����������������֪��ABC�ա�DBC��
���Զ�Ӧ��Ϊ����A=��D����ABC=��DBC����ACB=��DCB��
��Ӧ��Ϊ��AB=DB��AC=DC��BC=BC��
�ʴ�Ϊ���գ���A=��D����ABC=��DBC����ACB=��DCB��AB=DB��AC=DC��BC=BC.
�� ��A=��D����ABC=��DBC����ACB=��DCB AB��DB��AC��DC��BC��BC.
�����������������֪��ABC�ա�DBC��
���Զ�Ӧ��Ϊ����A=��D����ABC=��DBC����ACB=��DCB��
��Ӧ��Ϊ��AB=DB��AC=DC��BC=BC��
�ʴ�Ϊ���գ���A=��D����ABC=��DBC����ACB=��DCB��AB=DB��AC=DC��BC=BC. ��ͼ����������һ������б����ǽ�ϣ����Ӷ��˾����Ĵ�ֱ����MAΪa�ף���ʱ���ӵ���б��Ϊ75�㣬������б������һ��ǽʱ�����˾����Ĵ�ֱ����NBΪb�ף����ӵ���б��Ϊ45�㣬���������Ŀ�AB�Ƕ����ף�Ϊʲô��
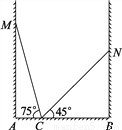
 a�ף�
���������������������BM��MN����SSS֤���գ��ɵá�CBM=��NBM=45�㣬AB=AM=a.
���������a�ף�����BM��MN��
�ڡ�MCN�У���MCN=180�㣭75�㣭45��=60�㣬CM=CN��
���MCN�ǵȱ������Σ�
��MC=MN����CBN=90�㣬��BCN=45�㣬
��BC=BN���ڡ�MCB�͡�MNB�У�
���MCB�ա�MNB��
...
a�ף�
���������������������BM��MN����SSS֤���գ��ɵá�CBM=��NBM=45�㣬AB=AM=a.
���������a�ף�����BM��MN��
�ڡ�MCN�У���MCN=180�㣭75�㣭45��=60�㣬CM=CN��
���MCN�ǵȱ������Σ�
��MC=MN����CBN=90�㣬��BCN=45�㣬
��BC=BN���ڡ�MCB�͡�MNB�У�
���MCB�ա�MNB��
... 
