题目内容
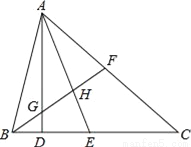
如图：（1）AD⊥BC，垂足为D，则AD是__的高，∠__=∠__=90°；
（2）AE平分∠BAC，交BC于点E，则AE叫__，∠__=∠__=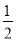
∠__，AH叫__；
（3）若AF=FC，则△ABC的中线是__；
（4）若BG=GH=HF，则AG是__的中线，AH是__的中线．
BC边上 ADB ADC ∠BAC的角平分线 BAE CAE BAC ∠BAF的角平分线 BF △ABH △AGF
【解析】试题解析：(1)AD⊥BC,垂足为D,则AD是BC边上的高,
(2)AE平分∠BAC,交BC于点E,则AE叫∠BAC的角平分线, AH叫∠BAF的角平分线；
(3)若AF=FC，则△ABC的中线是BF；
(4)若BG=GH=HF，则AG是△ABH的中线...
如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：
①（2a+b）（m+n）；②2a（m+n）+b（m+n）；③m（2a+b）+n（2a+b）；④2am+2an+bm+bn，你认为其中正确的有( )
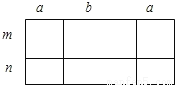
A. ①② B. ③④ C. ①②③ D. ①②③④
D
【解析】①大长方形的长为2a+b，宽为m+n，利用长方形的面积公式，表示即可；
②长方形的面积等于左边，中间及右边的长方形面积之和，表示即可；
③长方形的面积等于上下两个长方形面积之和，表示即可；
④长方形的面积由6个长方形的面积之和，表示即可．
解答：【解析】
①（2a+b）（m+n），本选项正确；
②2a（m+n）+b（m+n），本选项正确；
③m（2a+b）+n（... 计算：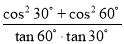 
+sin45°．
【解析】
试题分析：根据特殊角的三角函数值，可得实数的运算，根据实数的运算，可得答案．
试题解析：+sin45°
=
=2+
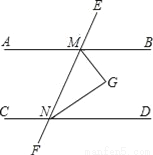
= 如图，AB∥CD，∠BMN与∠DNM的平分线相交于点G．
（1）完成下面的证明：
∵MG平分∠BMN
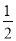∴∠GMN=
∠BMN
同理∠G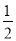NM=
∠DNM．
∵AB∥CD ，
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
（2）把上面的题设和结论，用文字语言概括为一个命题： ．
已知；角平分线的定义；已知；180°；90°；180°；90°；MG⊥NG.
【解析】试题分析：（1）根据平行线的性质进行填空即可；
（2）根据的特点作出结论．
试题解析：（1）∵MG平分∠BMN(已知)
(角平分线的定义)，
同理
∵ABCD(已知)，
∴MG与NG的位置关系是MG⊥NG；
故答案为：已知;角平分线的定义;已知; MG⊥NG；
(... 若三角形三个内角度数的比为2：3：4，则相应的外角比是__．
7：6：5
【解析】试题分析：由三角形的内角和是180°，三个内角的度数的比为2：3：4，可求得三个内角分别为40°，
60°，80°；从而对应的三个外角分别为140°，120°，100°；即可求得相应的的外角比. 下面说法正确的是个数有（ ）
①如果三角形三个内角的比是1：2：3，那么这个三角形是直角三角形；
②如果三角形的一个外角等于与它相邻的一个内角，则这么三角形是直角三角形；
③如果一个三角形的三条高的交点恰好是三角形的一个顶点，那么这个三角形是直角三角形；④如果∠A=∠B=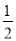
∠C，那么△ABC是直角三角形；⑤若三角形的一个内角等于另两个内角之差，那么这个三角形是直角三角形；⑥在△ABC中，若∠A+∠B=∠C，则此三角形是直角三角形．
A. 3个 B. 4个 C. 5个 D. 6个
D
【解析】试题分析：对各个选项逐一进行计算并判断，即可得出答案.
【解析】
①根据三角形三个内角的比是1：2：3，求出这个三角形的最大内角度数是 ，故这个三角形是直角三角形，故正确；
②三角形的一个外角等于与它相邻的一个内角，而三角形的这个外角与它相邻的内角的和为，故三角形的这个外角与它相邻的内角分别为，故这个三角形是直角三角形，故正确；
③因为直角三角形的两条直角边互... 若等腰三角形的一边是7，另一边是4，则此等腰三角形的周长是（ ）.
A．18 B．15 C．18或15 D．无法确定
C.
【解析】
试题分析：分情况讨论，假设7作腰长，则三边分别为7，7，4，周长为18；假设4作腰长，则三边分别为4，4，7，周长为15，所以此等腰三角形的周长是18或15.
故选：C. 公路BC所在的直线恰为AD的垂直平分线，则下列说法中：①小明从家到书店与小颖从家到书店一样远；②小明从家到书店与从家到学校一样远；③小颖从家到书店与从家到学校一样远；④小明从家到学校与小颖从家到学校一样远. 正确的是（）
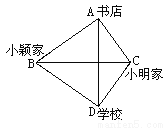
A. ①③ B. ②③ C. ②④ D. ③④
B
【解析】∵公路BC所在的直线恰为AD的垂直平分线，
∴ΔABC≌ΔDBC，
∴CA=CB，BA=BD，
故可判断出②小明从家到书店与从家到学校一样远；③小颖从家到书店与从家到学校一样远；
而无法判断出①小明从家到书店与小颖从家到书店一样远；④小明从家到学校与小颖从家到学校一样远，
故选B. 已知△ABC.求作：△A′B′C′，使△A′B′C′≌△ABC.
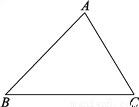
作图见解析
【解析】试题分析：本题可利用全等三角形的判定定理SSS作图，作AC=A′C′，A′B′=AB，BC=B′C′；根据全等三角形的判定可得△A′B′C′≌△ABC，注意尺规作图中作一条线段等于已知线段的作法．
试题解析：作法：①任意作一条射线B′M，以点B′为圆心，以BC为半径画弧，交射线于点C′；
②分别以点B′和点C′为圆心，以AB和AC为半径画弧，交于点A′，连接A...