题目内容
以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
 C
【解析】
试题解析:首先可以组合为13,10,5;13,10,7;13,5,7;10,5,7.再根据三角形的三边关系,发现其中的13,5,7不符合,则可以画出的三角形有3个.
故选C.
C
【解析】
试题解析:首先可以组合为13,10,5;13,10,7;13,5,7;10,5,7.再根据三角形的三边关系,发现其中的13,5,7不符合,则可以画出的三角形有3个.
故选C.
练习册系列答案
相关题目
小明计算一个二项式的平方时,得到正确结果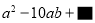 ,但最后一项不慎被污染了,这一项应
,但最后一项不慎被污染了,这一项应
是( ).
A. 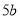 B.
B. 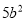 C.
C. 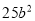 D.
D. 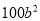
 C
【解析】试题解析:
∵?10ab=2a×(?5)×b,
∴最后一项为
故选C.
C
【解析】试题解析:
∵?10ab=2a×(?5)×b,
∴最后一项为
故选C. 已知在Rt△ABC中,∠C=90°,AC=4,cotA=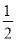 ,则BC的长是 .
,则BC的长是 .
 8
【解析】
试题分析:如图所示:
∵在Rt△ABC中,∠C=90°,AC=4,cotA=,
∴cotA==,
∴BC=8.
8
【解析】
试题分析:如图所示:
∵在Rt△ABC中,∠C=90°,AC=4,cotA=,
∴cotA==,
∴BC=8. 一个飞机零件的形状如图5—19所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,康师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
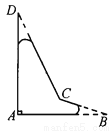
 不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格.
不合格,理由见解析.
【解析】试题分析:延长BC与AD相交于点E,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BCD即可判断.
试题解析:如图,延长BC与AD相交于点E,
∵∠1是△ABE的外角,
同理,
∵李师傅量得不是
∴这个零件不合格. 如图5—13,在△ABC中,AD⊥BC,GC⊥BC,CF⊥AB,BE⊥AC,垂足分别为D、C、F、E,则_______是△ABC中BC边上的高,_________是△ABC中AB边上的高,_________是 △ABC中AC边上的高,CF是△ABC的高,也是△_______、△_______、△_______、△_________的高.
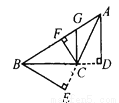
 AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC.
AD CF BE BFC FGC FAC GAC
【解析】试题解析:AD是△ABC中BC边上的高,是△ABC中AB边上的高,BE是△ABC中AC边上的高,CF是△ABC的高,也是△BFC、△FGC、△FAC、△GAC的高.
故答案是:AD、CF、BE、BFC、FGC、FAC、GAC. 三角形一个外角小于与它相邻的内角,这个三角形( )
A. 是直角三角形 B. 是锐角三角形
C. 是钝角三角形 D. 属于哪一类不能确定
 C
【解析】试题分析:锐角三角形的三个外角都大于与它相邻的内角;直角三角形的两个锐角的外角大于与它相邻的内角,直角的外角等于与它相邻的内角;钝角三角形的两个锐角的外角大于与它相邻的内角,钝角的外角小于与它相邻的内角.
C
【解析】试题分析:锐角三角形的三个外角都大于与它相邻的内角;直角三角形的两个锐角的外角大于与它相邻的内角,直角的外角等于与它相邻的内角;钝角三角形的两个锐角的外角大于与它相邻的内角,钝角的外角小于与它相邻的内角. 如图,△ABC中,D,E分别是BC上两点,且BD=DE=EC,则图中面积相等的三角形有( )
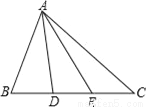
A. 4对 B. 5对 C. 6对 D. 7对
 A
【解析】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故选A.
A
【解析】等底同高的三角形的面积相等,所以△ABD,△ADE,△AEC三个三角形的面积相等,有3对,又△ABE与△ACD的面积也相等,有1对,所以共有4对三角形面积相等。
故选A. 如图,△ABC≌△AED,∠C=400,∠EAC=300,∠B=300,则∠EAD=( );
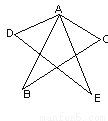
A. 300 B. 700 C. 400 D. 1100
 D
【解析】∵△ABC≌△AED,
∴∠D=∠C=40°,∠C=∠B=30°,
∴∠E AD=180°-∠D-∠E=110°,
故选D.
D
【解析】∵△ABC≌△AED,
∴∠D=∠C=40°,∠C=∠B=30°,
∴∠E AD=180°-∠D-∠E=110°,
故选D. 如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高______.
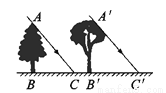
 6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),...
6米
【解析】试题解析:∵ AC∥A′C′
∴∠ACB=∠A′C′B′(两直线平行,同位角相等)
∵ 树木是垂直地面生长的,
∴∠ABC=∠A′B′C′=90°,
∵∠ABC=∠A′B′C′,∠ACB=∠A′C′B′,AC∥A′C′,
∴△ABC≌△A′B′C′(两角及其夹边对应相等的两个三角形全等),
∴AB=A′B′=6米 (全等三角形的对应边相等),... 
