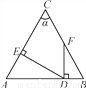
如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )
A. α B. 90°－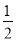
α C. 90°－α D. 180°－2α
B
【解析】∵∠A=∠B，∠C=α，
∴∠A=∠B=（180°-α），
∵DE⊥AC，FD⊥AB，
∴∠AED=∠FDB=90°，
∴∠ADE=90°-（180°-α）=α，
∴∠EDF =180°-90°-α=90°-α，
故选B． 一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF＝100°，那么∠BMD为( )
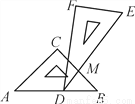
A. 95° B. 85° C. 90° D. 100°
B
【解析】∵∠ADF=100°，∠EDF=30°，
∴∠MDB=180°-∠ADF-∠EDF=180°-100°-30°=50°，
∴∠BMD=180°-∠B-∠MDB=180°-45°-50°=85°，
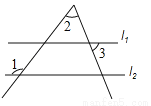
故选B. 如图，直线l1∥l2，若∠1=130°，∠2=60°，则∠3= ．
70°．
【解析】
试题分析：∵直线l1∥l2，∴∠4=∠1=130°，∴∠5=∠4﹣∠2=70°，∴∠5=∠3=70°．，故答案为：70°． 如图，以△ABC的顶点A为圆心，以BC长为半径作弧；再以顶点C为圆心，以AB长为半径作弧，两弧交于点D；连结AD、CD．若∠B=65°，则∠ADC的大小为______度.
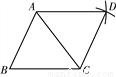
65
【解析】试题分析：∵以点A为圆心，以BC长为半径作弧；以顶点C为圆心，以AB长为半径作弧，两弧交于点D，
∴AB=CD，BC=AD，
在△ABC和△CDA中，
∵AB=CD，BC=AD，AC=CA，
∴△ABC≌△CDA（SSS），
∴∠ADC=∠B=65°．
故答案是65°． 如图是一副三角尺叠放的示意图，则∠α＝______．
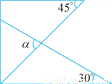
75°
【解析】如图，由已知可得∠1=45°，∴由三角形外角的性质可得：∠2=45°+30°=75°，
又∵∠=∠2，
∴∠=75°. 如图，已知△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B=40°，∠C=78°，则∠EAD=__°．
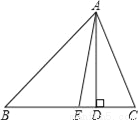
19
【解析】试题分析：根据三角形内角和定理称求得∠BAC，再由AE平分∠BAC，可求得∠EAC，最后由∠ADC=90°，∠C=78°，可求得∠DAC，即∠EAD可求. 一角为80°的三角形中，另两角的角平分线相交所成的锐角是________．
50°
【解析】∵∠A=80°，
∴∠ABC+∠ACB=180°-∠A=180°-80°=100°，
∵OB、OC分别是∠ABC、∠ACB的平分线，
∴∠OBC=∠ABC，∠OCB=∠ACB，
∴∠OBC+∠OCB=（∠ABC+∠ACB）=×100°=50°，
在△OBC中，∠BOC=180°-（∠OBC+∠OCB）=180°-50°=130°，
∴∠CO... 如图，在△ABC中，BD是边AC上的中线，E是BC的中点，连接DE.如果△BDE的面积为2，那么△ABC的面积为______．
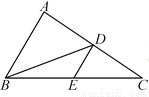
8
【解析】∵E是BC的中点,
∴ ,
∵BD是边AC上的中线,
∴ ,
∴,
又△BDE的面积为2，
∴△ABC的面积为8；
故答案是：8. 如图，点C，F在线段BE上，BF=EC，∠1=∠2，请你添加一个条件，使△ABC≌△DEF，并加以证明．（不再添加辅助线和字母）
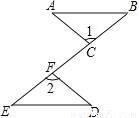
见解析
【解析】试题分析：先求出BC=EF，添加条件AC=DF，根据SAS推出两三角形全等即可．
AC=DF．
证明：∵BF=EC，
∴BF﹣CF=EC﹣CF，
∴BC=EF，
在△ABC和△DEF中
∴△ABC≌△DEF（SAS）． 如图，点B，F，C，E在直线l上（F，C之间不能直接测量），点A，D在l异侧，测得AB=DE，AC=DF，BF=EC.
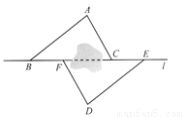
（1）求证：△ABC≌△DEF；
（2）指出图中所有平行的线段，并说明理由.
（1）详见解析；（2）∠ABC=∠DEF，∠ACB=∠DFE,理由见解析.
【解析】
试题分析：（1）理用SSS即可判定△ABC≌△DEF；（2）AB∥DE,AC∥DF,由全等三角形的性质可得∠ABC=∠DEF，∠ACB=∠DFE,根据平行线的性质即可得结论.
试题解析：（1）证明：∵BF=EC，
∴BF+CF=CF+CE，
∴BC=EF
∵AB=DE，AC=D...