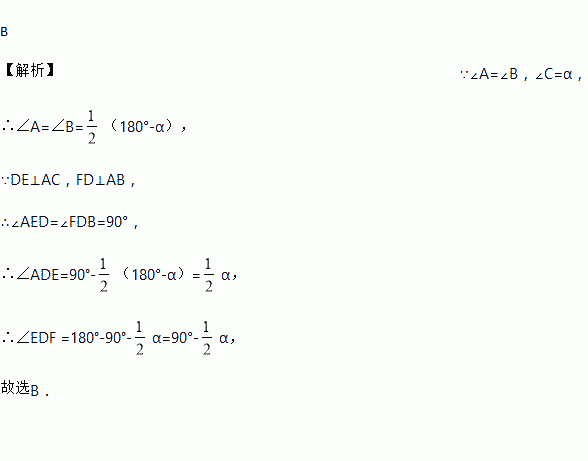题目内容
如图,∠A=∠B,∠C=α,DE⊥AC,FD⊥AB,则∠EDF等于( )
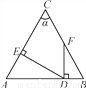
A. α B. 90°-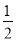 α C. 90°-α D. 180°-2α
α C. 90°-α D. 180°-2α
 B
【解析】∵∠A=∠B,∠C=α,
∴∠A=∠B=(180°-α),
∵DE⊥AC,FD⊥AB,
∴∠AED=∠FDB=90°,
∴∠ADE=90°-(180°-α)=α,
∴∠EDF =180°-90°-α=90°-α,
故选B.
B
【解析】∵∠A=∠B,∠C=α,
∴∠A=∠B=(180°-α),
∵DE⊥AC,FD⊥AB,
∴∠AED=∠FDB=90°,
∴∠ADE=90°-(180°-α)=α,
∴∠EDF =180°-90°-α=90°-α,
故选B.
练习册系列答案
相关题目
如图,在四边形ABCD中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
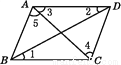
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠4 D. ∠4=∠5
 D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D.
D
【解析】A、当∠1=∠2时, AD∥BC ,故此选项错误;
B、当∠2=∠3时,无法得到AB∥CD,故此选项错误;
C、当∠3=∠4时,无法得到AB∥CD,故此选项错误;
D、当∠4=∠5时, AB∥CD,故此选项正确.
故选D. 如图,已知△ABE≌△ACD,且AB=AC.
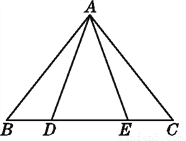
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
 (1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠...
(1)见解析;(2)∠BAD=∠CAE;(3)相等
【解析】试题分析:(1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
试题解析: (1)△ABE先水平翻转,再平移即可与△ACD重合;
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE?∠DAE=∠CAD?∠... 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
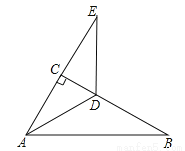
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
 30°;见解析.
【解析】试题分析:根据∠ACB和∠B的度数得出∠CAB的度数,根据角平分线的性质得出∠CAD的度数;根据∠ACD+∠ECD=180°,∠ACD=90°得出∠ACD=∠ECD=90°,证明△ACD和△ECD全等,从而得出结论.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°, ∴∠CAB=60°.
又∵AD平分∠CAB, ∴∠CAD=∠CAB=...
30°;见解析.
【解析】试题分析:根据∠ACB和∠B的度数得出∠CAB的度数,根据角平分线的性质得出∠CAD的度数;根据∠ACD+∠ECD=180°,∠ACD=90°得出∠ACD=∠ECD=90°,证明△ACD和△ECD全等,从而得出结论.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°, ∴∠CAB=60°.
又∵AD平分∠CAB, ∴∠CAD=∠CAB=... 如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=__°.
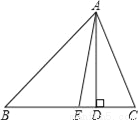
 19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求.
19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求. 在下列长度的四根木棒中,能与4cm、9cm长的两根木棒钉成一个三角形的是( )
A. 4cm B. 5cm C. 9cm D. 13cm
 C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C.
C
【解析】试题解析:根据三角形的三边关系,得:第三边应大于两边之差,且小于两边之和,
即9-4=5,9+4=13.
∴第三边取值范围应该为:5<第三边长度<13,
故只有C选项符合条件.
故选C. 已知a是-2的相反数,且|b+1|=0,则[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)的值为_____.
 5
【解析】[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)
=
=
=
∵a是-2的相反数,且|b+1|=0,
∴a=2,b=-1,
∴原式==-1+6=5.
5
【解析】[-3a2(ab2+2a)+4a(-ab)2]÷(-4a)
=
=
=
∵a是-2的相反数,且|b+1|=0,
∴a=2,b=-1,
∴原式==-1+6=5. 下列运算正确的是( )
A. 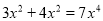 B.
B. 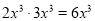 C.
C. 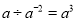 D.
D. 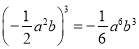
 C
【解析】根据合并同类项法则,可知,故不正确;
根据单项式乘以单项式和同底数幂相乘,可知,故不正确;
根据同底数幂相除,可知,故正确;
根据积的乘方,可知,故不正确.
故选:C.
C
【解析】根据合并同类项法则,可知,故不正确;
根据单项式乘以单项式和同底数幂相乘,可知,故不正确;
根据同底数幂相除,可知,故正确;
根据积的乘方,可知,故不正确.
故选:C. 如图OA⊥OC , OB⊥OD , 4位同学观察图形后分别说了自己的观点。
甲:∠AOB=∠COD; 乙:∠BOC+∠AOD = 1800;
丙:∠AOB+∠COD = 900; 丁:图中小于平角的角有5个;
其中正确的结论有( )
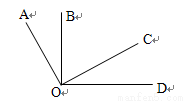
A.1个 B. 2个 C.3个 D.4个
 B
【解析】根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B.
B
【解析】根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B.