题目内容
如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
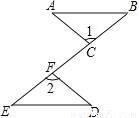
 见解析
【解析】试题分析:先求出BC=EF,添加条件AC=DF,根据SAS推出两三角形全等即可.
AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
见解析
【解析】试题分析:先求出BC=EF,添加条件AC=DF,根据SAS推出两三角形全等即可.
AC=DF.
证明:∵BF=EC,
∴BF﹣CF=EC﹣CF,
∴BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS).
练习册系列答案
相关题目
如图,已知∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由;
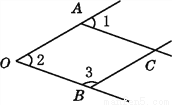
 AC//OB,OA//BC
【解析】试题分析:证明如下:如图所示,因为∠1=∠2,由“同位角相等,两直线平行”,可得AC//OB。又因为∠2=50°,∠3=130°,所以可得∠2=50°,∠3=130°,由“同旁内角互补,两直线平行”可得,OA//BC。
AC//OB,OA//BC;
理由: ∵∠1=50°,∠2=50° ( 已知 )
∴ ∠1=∠2
∴ AC//OB...
AC//OB,OA//BC
【解析】试题分析:证明如下:如图所示,因为∠1=∠2,由“同位角相等,两直线平行”,可得AC//OB。又因为∠2=50°,∠3=130°,所以可得∠2=50°,∠3=130°,由“同旁内角互补,两直线平行”可得,OA//BC。
AC//OB,OA//BC;
理由: ∵∠1=50°,∠2=50° ( 已知 )
∴ ∠1=∠2
∴ AC//OB... 如图,AD=BC,DC=AB,AE=CF,找出图中的一对全等三角形,并说明你的理由。
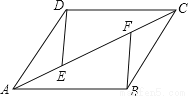
 △ABC≌△CDA
【解析】试题分析:全等三角形之一是△ABC≌△CDA,理由是根据AB=DC,AD=BC,AC=AC,根据全等三角形的判定定理SSS推出即可.
试题解析:△ABC≌△CDA.
理由是:在△ABC和△CDA中,
∵
∴△ABC≌△CDA(SSS).
△ABC≌△CDA
【解析】试题分析:全等三角形之一是△ABC≌△CDA,理由是根据AB=DC,AD=BC,AC=AC,根据全等三角形的判定定理SSS推出即可.
试题解析:△ABC≌△CDA.
理由是:在△ABC和△CDA中,
∵
∴△ABC≌△CDA(SSS). 如图所示,△ABC≌△CDA,AC=7 cm,AB=5 cm,BC=8 cm,则AD的长是( )
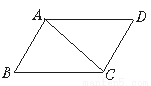
A.7 cm B.5 cm C.8 cm D.无法确定
 C
【解析】
试题分析:根据全等三角形的性质即可得到结果.
∵△ABC≌△CDA,
∴BC=AD=8 cm,
故选C.
C
【解析】
试题分析:根据全等三角形的性质即可得到结果.
∵△ABC≌△CDA,
∴BC=AD=8 cm,
故选C. 如图,有6个条形方格图,图中由实线围成的图形中,全等图形有:①与___________;②与___________.
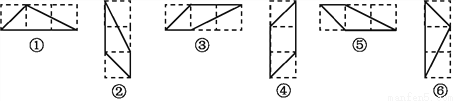
 ⑥ ③⑤
【解析】由全等图形的定义并观察图形可得①和⑥是全等图形,②、③和⑤是全等图形.
故答案为:⑥、③⑤
⑥ ③⑤
【解析】由全等图形的定义并观察图形可得①和⑥是全等图形,②、③和⑤是全等图形.
故答案为:⑥、③⑤ 如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连结AD、CD.若∠B=65°,则∠ADC的大小为______度.
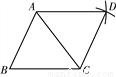
 65
【解析】试题分析:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD,
在△ABC和△CDA中,
∵AB=CD,BC=AD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=65°.
故答案是65°.
65
【解析】试题分析:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD,
在△ABC和△CDA中,
∵AB=CD,BC=AD,AC=CA,
∴△ABC≌△CDA(SSS),
∴∠ADC=∠B=65°.
故答案是65°. 在△ABC中,∠A=20°,∠B=60°,则△ABC的形状是( )
A. 等边三角形 B. 锐角三角形
C. 直角三角形 D. 钝角三角形
 D
【解析】试题分析:根据三角形的内角和定理求出∠C,即可判定△ABC的形状.
【解析】
∵∠A=20°,∠B=60°,
∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°,
∴△ABC是钝角三角形.
故选D.
D
【解析】试题分析:根据三角形的内角和定理求出∠C,即可判定△ABC的形状.
【解析】
∵∠A=20°,∠B=60°,
∴∠C=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°,
∴△ABC是钝角三角形.
故选D. 如果(2x+m)(x-5)展开后的结果中不含x的一次项,那么m等于( )
A. 5 B. -10 C. -5 D. 10
 D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D.
D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D. (1)完成下列各题计算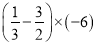
(2)计算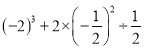
(3)已知A=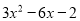 ,B=
,B=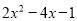 ,求A-2B
,求A-2B
 (1)7,(2)-7,(3)
【解析】试题分析:(1)利用乘法的分配率进行计算即可;
(2)先算乘方,然后计算乘除,最后计算加法即可;
(3)把A、B代入,去掉括号,然后合并同类项即可.
试题解析:
【解析】
(1)原式=×(-6)+()×(-6)
=-2+9
=7;
(2)原式=-8+2××2
=-8+1
=-7;
(3)A-2...
(1)7,(2)-7,(3)
【解析】试题分析:(1)利用乘法的分配率进行计算即可;
(2)先算乘方,然后计算乘除,最后计算加法即可;
(3)把A、B代入,去掉括号,然后合并同类项即可.
试题解析:
【解析】
(1)原式=×(-6)+()×(-6)
=-2+9
=7;
(2)原式=-8+2××2
=-8+1
=-7;
(3)A-2... 
