题目内容
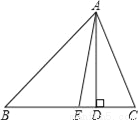
如图，已知△ABC中，AD是BC边上的高，点E在线段BD上，且AE平分∠BAC，若∠B=40°，∠C=78°，则∠EAD=__°．
19
【解析】试题分析：根据三角形内角和定理称求得∠BAC，再由AE平分∠BAC，可求得∠EAC，最后由∠ADC=90°，∠C=78°，可求得∠DAC，即∠EAD可求.
练习册系列答案
相关题目
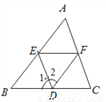
如图，（1）如果∠1=__________，那么DE∥AC；（同位角相等，两直线平行）；
（2）如果∠1=__________，那么EF∥BC；（内错角相等，两直线平行）；
（3）如果∠DEF+__________=180°，那么DE∥AC；（同旁内角互补，两直线平行）；
（4）如果∠2+__________=180°，那么AB∥DF；（同旁内角互补，两直线平行）．
∠C； ∠DEF； ∠EFC； ∠AED．
【解析】（1）如果∠1=∠C ，那么DE//AC；（同位角相等，两直线平行）
（2）如果∠1=∠DEF ，那么EF//BC；（内错角相等，两直线平行）
（3）如果∠DEF+∠EFC =180°，那么DE//AC；（同旁内角互补，两直线平行）
（4）如果∠2+∠AED =180°，，那么AB//DF；（同旁内角互补，两直线平行）
... 如图，AB=CD，AD=CB，那么下列结论中错误的是（ ）
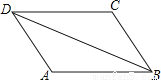
A. ∠A=∠C B. AB=AD C. AD∥BC D. AB∥CD
B
【解析】∵在△ABD和△CDB中，
，
∴△ABD≌△CDB，
∴∠ADB=∠CBD，∠ABD=∠CDB，∠A=∠C
∴AD∥BC，AB∥CD，
∴A、C、D选项正确.
故选：B. 如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌___________,AB的对应边是___________,∠BCA的对应角是___________.
△ADC AD ∠DCA
【解析】本题考查的是全等三角形的性质
根据全等三角形的对应边相等、对应角相等即可判断， （10分）在△ABC中，BE、CF分别是AC、AB两条边上的高，在BE上截取BD＝AC，在CF的延长线上截取CG＝AB，连结AD、AG。求证：AG＝AD
可证明△EBM≌△FCM，
得∠EMB≌△FCM，
得∠EMB＝∠FMC，
∵∠CMF＋∠BMF＝180°
∴∠BME＋∠BMF＝180°
∴E、F、M恰好在一直线上
【解析】分析：三角形全等条件中必须是三个元素，本题已经有两条对应边相等，只要再找到它们的夹角相等就可以了．
解答：证明：∵BE、CF分别是AC、AB两条边上的高，
∴∠ABD+∠BAC... 如图，∠A＝∠B，∠C＝α，DE⊥AC，FD⊥AB，则∠EDF等于( )
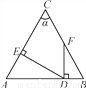
A. α B. 90°－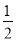
α C. 90°－α D. 180°－2α
B
【解析】∵∠A=∠B，∠C=α，
∴∠A=∠B=（180°-α），
∵DE⊥AC，FD⊥AB，
∴∠AED=∠FDB=90°，
∴∠ADE=90°-（180°-α）=α，
∴∠EDF =180°-90°-α=90°-α，
故选B． 已知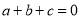
， 
.
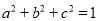（1）求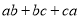
的值；
（2）求
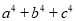的值．
（1） （2）
【解析】试题分析：（1）把a+b+c=0两边平方，然后利用代入法等量代换即可；
（2）把ab+bc+ca与两边分别乘方即可.
试题解析：（1）因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
（2）因为a+b+c=0，a2+b2+c2=1
所以+2ab+2ac+2bc=0
... 若□×3xy＝3x2y，则□内应填的单项式是( )
A. xy B. 3xy C. x D. 3x
C
【解析】试题分析：根据题意列出算式，计算即可得到结果．
【解析】
根据题意得：3x2y÷3xy=x，
故选：C 如图，已知三角形ABC中有正方形EDFC，请你简述三角形AED到三角形PFD的变化过程是：_____________________________________
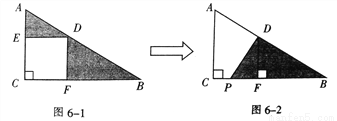
以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析：由图可知三角形AED到三角形PFD，点D位置不变，点A至点P，点E至点F，AD＝PD，ED＝FD，根据旋转的性质可知：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD．
故答案为：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD．