17. 若关于x的不等式x-m>-1的解集如图所示,则m等于( )
若关于x的不等式x-m>-1的解集如图所示,则m等于( )
 若关于x的不等式x-m>-1的解集如图所示,则m等于( )
若关于x的不等式x-m>-1的解集如图所示,则m等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完全这件事的不同办法数是各类不同方法种树的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分别几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分布计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
小王想获得至少30分的加分,那么概率为多少?
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
12.根据下表回答下列问题:
(1)(6×10)3=63×103.(6×0.1)3=63×($\frac{1}{10}$)3.
(2)12.167的立方根是2.3.
(3)$\root{3}{-9.261}$=-2.1.
0 282503 282511 282517 282521 282527 282529 282533 282539 282541 282547 282553 282557 282559 282563 282569 282571 282577 282581 282583 282587 282589 282593 282595 282597 282598 282599 282601 282602 282603 282605 282607 282611 282613 282617 282619 282623 282629 282631 282637 282641 282643 282647 282653 282659 282661 282667 282671 282673 282679 282683 282689 282697 366461
| x | 0.6 | 6 | 60 | 2 | 2.1 | 2.2 | 2.3 | 2.4 |
| x3 | 0.216 | 216 | 216000 | 8 | 9.261 | 10.648 | 12.167 | 13.824 |
(2)12.167的立方根是2.3.
(3)$\root{3}{-9.261}$=-2.1.
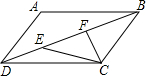 如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.
如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.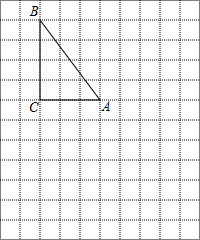 在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,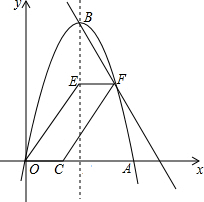 如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.
如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.