题目内容
14.完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完全这件事的不同办法数是各类不同方法种树的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分别几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分布计数原理,也叫做乘法原理.(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.
| 加分 | 人数 |
| 10 | 30 |
| 20 | 90 |
| 30 | 150 |
| 60 | 30 |
(Ⅱ)某大学的录取分数线为660分,小王估得高于分数可能在630-639,640-649,650-659三个分段.
(1)若小王的高考分数在630-639分段,则小王被该大学录取的概率为多少?
(2)若小王的高考分数在三个片段的概率都是$\frac{1}{3}$,则小王被该大学录取的概率为多少?
分析 完成一件事有几类办法,各类办法相互独立,每类办法中又有多种不同的办法,则完成这件事的不同办法数是各类不同方法种数的和,这就是分类计数原理,也叫做加法原理.完成一件事,需要分成几个步骤,每一步的完成有多种不同的方法,则完成这件事的不同方法种数是各种不同的方法数的乘积,这就是分步计数原理,也叫做乘法原理.
(Ⅰ)300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次.获得至少30分的加分的人数有180人,由此能求出小王获得至少30分的加分的概率.
(Ⅱ)(1)小王被该大学录取,需要获得至少30分的加分,由此能求出小王被该大学录取的概率.
(2)利用相互独立事件概率乘法公式和互斥事件概率加法公式能求出小王被该大学录取的概率.
解答 解:(Ⅰ)∵300人参加校内竞赛,每个人都可以享受加分政策,且有10,20,30,60四个档次,
获得至少30分的加分的人数有:150+30=180,
∴小王获得至少30分的加分的概率为:p1=$\frac{180}{300}$=$\frac{3}{5}$.
(Ⅱ)(1)∵某大学的录取分数线为660分,小王的高考分数在630~639分段,
∴小王被该大学录取,需要获得至少30分的加分,
∴小王被该大学录取的概率为p2=$\frac{180}{300}$=$\frac{3}{5}$.
(2)∵某大学的录取分数线为660分,小王估得高考分数可能在630~639,640~649,650~659三个分段,
小王的高考分数在三个分段的概率都是$\frac{1}{3}$,
∴小王被该大学录取的概率为p3=$\frac{1}{3}$×$\frac{3}{5}$+$\frac{1}{3}$×$\frac{9}{10}$+$\frac{1}{3}$×1=$\frac{5}{6}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式、相互独立事件概率乘法公式和互斥事件概率加法公式的合理运用.

 名校课堂系列答案
名校课堂系列答案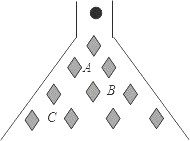 在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$.
在科技馆里,小亮看见一台名为帕斯卡三角的仪器,如图所示,当一实心小球从入口落下,它在依次碰到每层菱形挡块时,会等可能地向左或向右落下.试问小球下落到第三层B位置的概率是$\frac{5}{8}$. 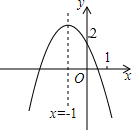 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①3a+2b+c<0;
②3a+c<b2-4ac;
③方程2ax2+2bx+2c-5=0没有实数根;
④m(am+b)+b<a(m≠-1).
其中正确结论的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
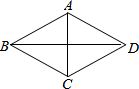 如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )
如图,菱形ABCD中,AB=5,∠BCD=120°,则对角线BD的长是( )| A. | 5 | B. | 10 | C. | 5$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
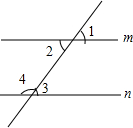 如图,请写出一个能使m∥n的条件∠2=∠3.
如图,请写出一个能使m∥n的条件∠2=∠3.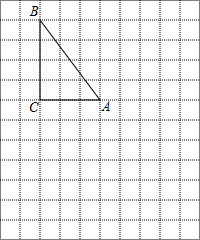 在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,
在下面的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,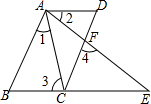 如图,若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?并请说明理由.
如图,若AB∥CD,∠1=∠2,∠3=∠4,AD与BC平行吗?并请说明理由.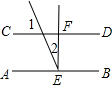 如图,AB∥CD,EF⊥CD于E,EF交CD于F,已知∠1=63°,则∠2=27°.
如图,AB∥CD,EF⊥CD于E,EF交CD于F,已知∠1=63°,则∠2=27°.