题目内容
16．已知（x+y）2=1，（x-y）2=49，求x2+y2与xy的值．分析 已知等式利用完全平方公式化简，相加减即可求出所求式子的值．
解答 解：∵（x+y）2=x2+y2+2xy=1①，（x-y）2=x2+y2-2xy=49②，
∴①+②得：2（x2+y2）=50，即x2+y2=25；
①-②得：4xy=-48，即xy=-12．
点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
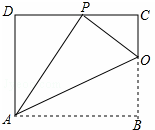已知：如图，矩形ABCD的一条边AB=10，将矩形ABCD折叠，使得顶点B落在CD边上的P点处，折痕为AO．
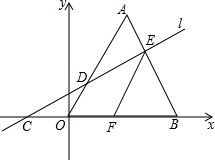如图，在平面直角坐标系中，△A0B是边长为3的等边三角形，直线l与x轴、0A、AB分别交于点C、D、E，0C=AE．过点E作EF∥0A，交x轴于点F．
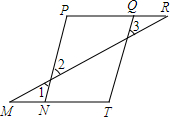如图，M、N、T和A、B、C分别在同一直线上，且∠1=∠3，∠P=∠T，求证：PQ∥MT．
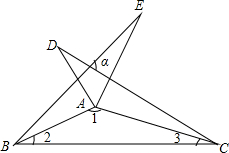如图，把△ABC沿AB、AC翻折180°得到△ABE、△ACD，若∠1：∠2：∠3=28：5：3，则∠α的度数为80°．
8．比较（27）4与（34）3的大小，可得（ ）
| A． | （27）4=（34）3 | B． | （27）4＞（34）3 | C． | （27）4＜（34）3 | D． | 无法确定 |
5．把$\sqrt{\frac{27}{4}}$化为最简二次根式，结果是（ ）
| A． | $\frac{\sqrt{27}}{2}$ | B． | $\frac{3\sqrt{3}}{\sqrt{4}}$ | C． | $\frac{3}{2}$ | D． | $\frac{3\sqrt{3}}{2}$ |