题目内容
20.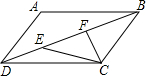 如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.
如图,在?ABCD中,∠ADB=2∠BDC,点E为对角线BD上一点,CF垂直平分线段BE,连接EC.求证:DE=BC.
分析 由平行四边形的性质得出AD∥BC,得出∠DBC=∠ADB=2∠BDC,由线段垂直平分线的性质得出CE=CB,得出∠CEB=∠CBE,因此∠CEB=2∠BDC,由三角形的外角性质得出∠BDC=∠ECD,证出ED=EC,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DBC=∠ADB=2∠BDC,
∵CF垂直平分线段BE,
∴CE=CB,
∴∠CEB=∠CBE,
∴∠CEB=2∠BDC,
∵∠CEB=∠BDC+∠ECD,
∴∠BDC=∠ECD,
∴ED=EC,
∴ED=BC.
点评 本题考查了平行四边形的性质、线段垂直平分线的性质、三角形的外角性质、等腰三角形的判定与性质;熟练掌握平行四边形的性质,证明ED=EC是解决问题的关键.

练习册系列答案
相关题目
9.在数轴上表示不等式3x+1≥4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
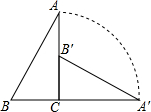 如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.
如图,已知△ABC中∠A=30°,∠C=90°,AB=4,将△ABC绕点C顺时针旋转90°得到△A′B′C′.在整个旋转过程中.