题目内容
13.已知函数y=-x2的图象向右平移2个单位,再向上平移n(n>0)个单位后得到的抛物线C恰好与直线y=-2x+8相切与点A.(1)求抛物线C得解析式;
(2)若抛物线C的顶点为B,交y轴与点D,△ABD的外接圆交x轴与M、N两点,求MN的长.
分析 (1)设抛物线C的解析式为y=-(x-2)2+n(n>0).把y=-x+8代入y=-(x-2)2+n得到的关于x的二元一次方程(含n),接下来,依据方程有两个相等的实数根可求得n的值,从而得到抛物线的解析式
(2)圆E为△ABD的外接圆,连接ME、NE,过点E作EF⊥MN,垂足为F.先求得点A、B、D的坐标,然后依据由两点间的距离公式可知AD、BD、AB的长,然后依据勾股定理的逆定理可知△ABD为直角三角形,从而可得到点E的坐标和圆E的半径,接下来,依据勾股定理可求得MF的长,最后依据垂径定理可求得MN的长.
解答 解:(1)设抛物线C:y=-(x-2)2+n(n>0).
将y=-x+8代入y=-(x-2)2+n得:-(x-2)2+n=-x+8,整理得:x2-6x+12-n=0,
∵直线与抛物线相切,
∴△=36-4(12-n)=0,解得:n=3.
∴抛物线C的解析式为y=-(x-2)2+3,即y=-x2+4x-1.
(2)如图所示:圆E为△ABD的外接圆,连接ME、NE,过点E作EF⊥MN,垂足为F.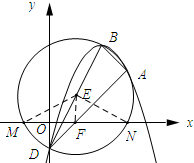
∵令x=0得y=-1,
∴D(0,-1).
由抛物线的解析式可知:B(2,3).
∵由(1)可知:当n=3时,直线与抛物线相切,
∴x2-6x+9=0,解得:x=3.
∵将x=3代入y=-2x+8得:y=2,
∴A(3,2).
∵由两点间的距离公式可知AD2=(3-0)2+(-1-2)2=18,BD2=(2-0)2+(-1-3)2=20,AB2=(3-2)2+(2-3)2=2,
∴BD2=BA2+AD2.
∴三角形ABD为直角三角形.
∵圆E是△ABD的外接圆,
∴E是BD的中点.
∴E(1,1).
∴ME=DE=$\frac{1}{2}$BD=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$,EF=1.
∵EF⊥MN,
∴MF=FN,∠EFM=90°.
在Rt△MEF中,MF=$\sqrt{M{E}^{2}-E{F}^{2}}$=2.
∴MN=2MF=4.
∴MN的长度为4.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了平移与坐标变换的关系、一元二次方程根据判别式、勾股定理的逆定理、勾股定理、垂径定理等知识,求得点E的坐标可圆E的半径的长度是解题的关键.

 小题狂做系列答案
小题狂做系列答案| A. | x2=-2 | B. | (x+2)2=x(x-1) | C. | $\frac{1}{{x}^{2}}$$+\frac{2}{x}$=1 | D. | x2-2x+y=0 |
| A. | 邻补角一定互补 | |
| B. | 不重合的两条直线只有两种位置关系:相交和平行 | |
| C. | 对顶角相等 | |
| D. | 垂线段最短 |
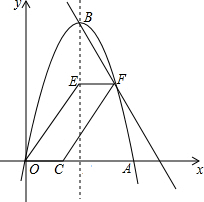 如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.
如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.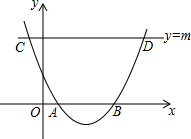 如图所示的抛物线与x轴交于A、B两点,与直线y=m交于C、D两点,请仅用没有刻度的直尺作出该抛物线的对称轴l.(保留作图痕迹,不写作法)
如图所示的抛物线与x轴交于A、B两点,与直线y=m交于C、D两点,请仅用没有刻度的直尺作出该抛物线的对称轴l.(保留作图痕迹,不写作法)