题目内容
18.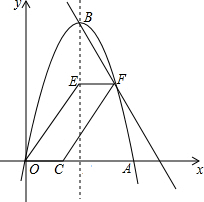 如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.
如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.(1)求B点坐标;
(2)当tan∠EOC=$\frac{4}{3}$时,显然满足条件的四边形有两个,求出相应的点F的坐标;
(3)当0<tan∠EOC<3时,对于每一个确定的tan∠EOC值,满足条件的四边形OCFE有两个,当这两个四边形的面积之比为1:2时,求tan∠EOC.
分析 (1)利用配方法把一般式配成顶点式即可得到B点坐标;
(2)抛物线的对称轴为直线x=3,直线x=3交x轴于H,如图,利用正切定义可计算出EH,从而得到E点坐标为(3,4)或(3,-4),然后分别计算函数值为4和-4所对应的自变量的值即可得到满足条件的F点的坐标;
(3)如图,利用平行四边形OEFC和平行四边形OE′F′C′等高得到OC′=2OC,则可设OC=t,则OC′=2t,于是得到F点的横坐标为3+t,F′点的横坐标为3+2t,然后利用点F和F′的纵坐标互为相反数可列方程-(3+t-3)2+9+[-(3+2t-3)2+9]=0,解方程求出t的值,则可得到F点的坐标,从而得到E点坐标,最后利用正切的定义求解.
解答 解:(1)∵y=-x2+6x=-(x-3)2+9,
∴B(3,9);
(2)抛物线的对称轴为直线x=3,直线x=3交x轴于H,如图,
∵tan∠EOC=$\frac{4}{3}$,即tan∠EOH=$\frac{4}{3}$,
∴$\frac{EH}{OH}$=$\frac{4}{3}$,
∴EH=4,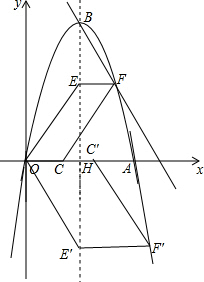
∴E点坐标为(3,4)或(3,-4),
当y=4时,-(x-3)2+9=4,解得x1=3-$\sqrt{5}$(舍去),x2=3+$\sqrt{5}$,
当y=-4时,-(x-3)2+9=-4,解得x1=3-$\sqrt{13}$(舍去),x2=3+$\sqrt{13}$,
∴F点坐标为(3+$\sqrt{5}$)或(3+$\sqrt{13}$,-4);
(3)如图,∵平行四边形OEFC和平行四边形OE′F′C′等高,
∴这两个四边形的面积之比为1:2时,OC′=2OC,
设OC=t,则OC′=2t,
∴F点的横坐标为3+t,F′点的横坐标为3+2t,
而点F和F′的纵坐标互为相反数,
∴-(3+t-3)2+9+[-(3+2t-3)2+9]=0,解得t1=$\frac{3\sqrt{10}}{5}$,t2=-$\frac{3\sqrt{10}}{5}$(舍去),
∴F点坐标为(3+$\frac{3\sqrt{10}}{5}$,$\frac{27}{5}$),
∴E(3,$\frac{27}{5}$),
∴tan∠EOC=$\frac{\frac{27}{5}}{3}$=$\frac{9}{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的性质;理解坐标与图形性质以及锐角三角函数的定义;会解一元二次方程;学会运用分类讨论的思想解决数学问题.

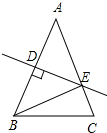 在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )
在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,若∠EBC=30°,则∠A的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
| A. | m2+(-n)2 | B. | m2-m+1 | C. | m2-n | D. | m2-2m+1 |
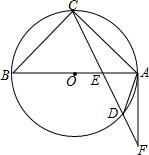 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求:
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作⊙O的切线与CD长线交于点F,AC=8,CE:ED=6:5,AE:EB=2:3.求: