18.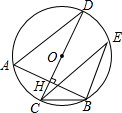 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
 如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )
如图,AB为⊙O的弦,CD为直径,且CD⊥AB于H,∠E=30°,CB=3,则AD的长为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
16.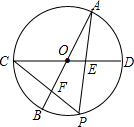 如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
 如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB,CD是⊙O的两条直径,∠AOC=120°,P是弧BD上的任意一点(不与点B,D重合),AP,CP分别交CD,AB于点E,F.若S△AOE+S△COF=2$\sqrt{3}$,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
15. 如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
 如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
14. 如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
 如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )| A. | $\frac{1}{2}$或$-\frac{1}{2}$ | B. | $\frac{1}{3}$或$-\frac{1}{3}$ | C. | $\frac{3}{4}$或$-\frac{3}{4}$ | D. | $\frac{2}{3}$或$-\frac{2}{3}$ |
13.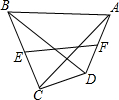 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
0 281454 281462 281468 281472 281478 281480 281484 281490 281492 281498 281504 281508 281510 281514 281520 281522 281528 281532 281534 281538 281540 281544 281546 281548 281549 281550 281552 281553 281554 281556 281558 281562 281564 281568 281570 281574 281580 281582 281588 281592 281594 281598 281604 281610 281612 281618 281622 281624 281630 281634 281640 281648 366461
 如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )
如图所示:在四边形ABCD中,对角线AC⊥BD,且AC=$2\sqrt{3}$,BD=6,E、F分别是BC、AD的中点,则EF=( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 6 | D. | $\frac{3}{2}\sqrt{3}$ |
 如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.
如图所示,正方形ABCD的边长为2,点E、F分别为边AB、AD 的中点,点G是CF上的一点,使得3CG=2GF,则三角形BEG的面积为$\frac{4}{5}$.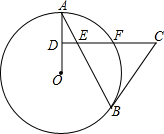 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
