题目内容
20.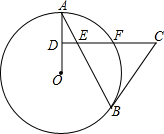 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.(1)求证:BC是⊙O的切线;
(2)连接AF、BF,求∠ABF的度数;
(3)如果CD=15,sinA=$\frac{5}{13}$,求⊙O的半径.
分析 (1)连接OB,由圆的半径相等和已知条件证明∠OBC=90°,即可证明BC是⊙O的切线;
(2)连接OF,AF,BF,首先证明△OAF是等边三角形,再利用圆周角定理:同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数;
(3)如图,延长CD交⊙O于M.设OA=r,则AD=$\frac{1}{2}$r.DE=$\frac{5}{24}$r,DF=DM=$\frac{\sqrt{3}}{2}$r,CF=15-$\frac{\sqrt{3}}{2}$r,CE=CB=15-$\frac{5}{24}$r.
根据BC2=CF•CM,列出方程即可解决问题.
解答 (1)证明:连接OB,
∵OB=OA,CE=CB,
∴∠A=∠OBA,∠CEB=∠ABC,
又∵CD⊥OA,
∴∠A+∠AED=∠A+∠CEB=90°,
∴∠OBA+∠ABC=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(2)解:如图1,连接OF,AF,BF,
∵DA=DO,CD⊥OA,
∴AF=OF,
∵OA=OF,
∴△OAF是等边三角形,
∴∠AOF=60°,
∴∠ABF=$\frac{1}{2}$∠AOF=30°;
(3)解:如图,延长CD交⊙O于M.设OA=r,则AD=$\frac{1}{2}$r.DE=$\frac{5}{24}$r,DF=DM=$\frac{\sqrt{3}}{2}$r,CF=15-$\frac{\sqrt{3}}{2}$r,CE=CB=15-$\frac{5}{24}$r.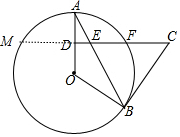
∵BC2=CF•CM,
∴(15-$\frac{5}{24}$r)2=(15-$\frac{\sqrt{3}}{2}$r)(15+$\frac{\sqrt{3}}{2}$r),
解得r=$\frac{3600}{457}$
点评 此题考查了切线的判定,以及相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.

 如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )
如图,AB⊥AC,CD平分∠ACB,BE平分∠ABC,AG∥BC,AG⊥BG.下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=2∠ACD;④∠ABE=∠ACD,其中正确的结论是( )| A. | ①③ | B. | ②④ | C. | ①②③ | D. | ①②③④ |
 如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )
如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |