��Ŀ����
14�� ��ͼ������ABCD�ı�AB��x���ϣ�AB���е���ԭ��O�غϣ�AB=2��AD=1����Q������Ϊ��0��2������P��x��0���ڱ�AB���˶���������Q��P��ֱ�߽�����ABCD���ܳ��ֳ�2��1�����֣���x��ֵΪ��������
��ͼ������ABCD�ı�AB��x���ϣ�AB���е���ԭ��O�غϣ�AB=2��AD=1����Q������Ϊ��0��2������P��x��0���ڱ�AB���˶���������Q��P��ֱ�߽�����ABCD���ܳ��ֳ�2��1�����֣���x��ֵΪ��������| A�� | $\frac{1}{2}$��$-\frac{1}{2}$ | B�� | $\frac{1}{3}$��$-\frac{1}{3}$ | C�� | $\frac{3}{4}$��$-\frac{3}{4}$ | D�� | $\frac{2}{3}$��$-\frac{2}{3}$ |
���� �������ۣ���P��OA�Ϻ͵�P��OB��������������������г�������ϵʽ��ֱ�ӽ�ɵó�x�ó�ֵ��
��� �⣺��ͼ����AB���е���ԭ��O�غϣ��ھ���ABCD�У�AB=2��AD=1��
��A��-1��0����B��1��0����C��1��1����
����P��OB��ʱ������G��$\frac{x}{2}$��1��
�߹���Q��P��ֱ�߽�����ABCD���ܳ��ֳ�2��1�����֣�
��AP+AD+DG=3+$\frac{3}{2}$x��CG+BC+BP=3-$\frac{3}{2}$x��
������ɵã�3+$\frac{3}{2}$x=2��3-$\frac{3}{2}$x����
���x=$\frac{2}{3}$��
�ɶԳ��Կ���P��OA��ʱ��x=-$\frac{2}{3}$��
��ѡD��
���� ������Ҫ������һ�κ������ۺ��⣬���Ҫע�����ν��˼������ã��Ǹ����п����ȵ㣬ͬѧ��Ҫ��ǿѵ���������е��⣮

��ϰ��ϵ�д�
�����Ŀ
2��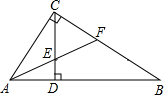 ��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D��AFƽ�֡�CAB����CD��E����BC��F����AF=BF����֤����CEF�ǵȱ������Σ�
��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D��AFƽ�֡�CAB����CD��E����BC��F����AF=BF����֤����CEF�ǵȱ������Σ�
 ��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D��AFƽ�֡�CAB����CD��E����BC��F����AF=BF����֤����CEF�ǵȱ������Σ�
��ͼ����Rt��ABC�У���ACB=90�㣬CD��AB��D��AFƽ�֡�CAB����CD��E����BC��F����AF=BF����֤����CEF�ǵȱ������Σ�
2��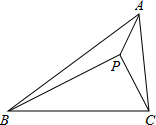 ��ͼ����ABC�У���BAC=60�㣬AB=2AC����P�ڡ�ABC�ڣ���PA=$\sqrt{3}$��PB=5��PC=2�����ABC�����Ϊ��������
��ͼ����ABC�У���BAC=60�㣬AB=2AC����P�ڡ�ABC�ڣ���PA=$\sqrt{3}$��PB=5��PC=2�����ABC�����Ϊ��������
 ��ͼ����ABC�У���BAC=60�㣬AB=2AC����P�ڡ�ABC�ڣ���PA=$\sqrt{3}$��PB=5��PC=2�����ABC�����Ϊ��������
��ͼ����ABC�У���BAC=60�㣬AB=2AC����P�ڡ�ABC�ڣ���PA=$\sqrt{3}$��PB=5��PC=2�����ABC�����Ϊ��������| A�� | 3+$\frac{7}{2}$$\sqrt{3}$ | B�� | 3+$\frac{5}{2}$$\sqrt{3}$ | C�� | 3+$\sqrt{3}$ | D�� | 3+$\frac{1}{2}$$\sqrt{3}$ |
4��ѧϰ��һ�κ�����С��������������һ����ӱ�ĺ�����y=|x-1|��С�ٸ���ѧУ�����ľ��飬�Ժ���y=|x-1|��ͼ�������ʽ�����̽����������С�ٵ�̽�����̣��벹����ɣ�
��1���б����±���y��x�ļ����Ӧֵ���벹��������
��2��������ߣ���ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��3����һ��̽�����֣��ú���ͼ�����͵�������ǣ�1��0������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ�����x��0ʱ��y��x���������С��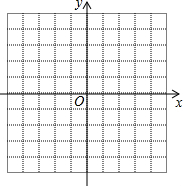
��1���б����±���y��x�ļ����Ӧֵ���벹��������
| x | �� | -3 | -2 | -1 | 0 | 1 | 2 | 3 | �� |
| y | �� | 4 | 3 | 2 | 1 | 0 | 1 | 2 | �� |
��3����һ��̽�����֣��ú���ͼ�����͵�������ǣ�1��0������Ϻ�����ͼ��д���ú������������ʣ�һ�����ɣ�����x��0ʱ��y��x���������С��

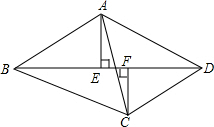 ��ͼ�����ı���ABCD�У�AE��BD��CF��BD����AE=CF����BAC=��DCA����֤���ı���ABCD��ƽ���ı��Σ�
��ͼ�����ı���ABCD�У�AE��BD��CF��BD����AE=CF����BAC=��DCA����֤���ı���ABCD��ƽ���ı��Σ�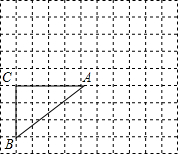 ��������ͼ�У�ÿ��С�����α߳���Ϊ1����λ����Rt��ABC�У�AC=4��BC=3����C=90�㣮����B������Ϊ��-3��-3��������ͼ�л���ƽ��ֱ������ϵ������������������ϵ���ڸ������������������ABCλ�Ƶġ�A1B1C1��ʹ��λ������Ϊԭ�㣬��A1B1C1���ABC�����Ʊ���2����д��A1��B1��C1������꣮
��������ͼ�У�ÿ��С�����α߳���Ϊ1����λ����Rt��ABC�У�AC=4��BC=3����C=90�㣮����B������Ϊ��-3��-3��������ͼ�л���ƽ��ֱ������ϵ������������������ϵ���ڸ������������������ABCλ�Ƶġ�A1B1C1��ʹ��λ������Ϊԭ�㣬��A1B1C1���ABC�����Ʊ���2����д��A1��B1��C1������꣮
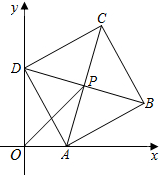 ��֪����ͼ��ƽ��ֱ������ϵxOy�У�������ABCD�ı߳�Ϊ4�����Ķ���A��x������������˶�����A��D������ԭ���غϣ�������B��C���ڵ�һ���ޣ��ҶԽ���AC��BD�ཻ�ڵ�P������OP�����P��y��ľ���Ϊd�����ڵ�A��D�˶��Ĺ����У�d��ȡֵ��Χ��2��d��2$\sqrt{2}$��
��֪����ͼ��ƽ��ֱ������ϵxOy�У�������ABCD�ı߳�Ϊ4�����Ķ���A��x������������˶�����A��D������ԭ���غϣ�������B��C���ڵ�һ���ޣ��ҶԽ���AC��BD�ཻ�ڵ�P������OP�����P��y��ľ���Ϊd�����ڵ�A��D�˶��Ĺ����У�d��ȡֵ��Χ��2��d��2$\sqrt{2}$��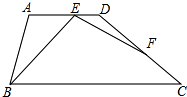 ��ͼ������ABCD�У�AD��BC����ABC=2��BCD=2������F��DC�ϣ��ҡ�BEF=��A��
��ͼ������ABCD�У�AD��BC����ABC=2��BCD=2������F��DC�ϣ��ҡ�BEF=��A��