题目内容
19.在Rt△ABC中,AB=6,∠B=90°,BC=8,点P从A出发沿AC方向在运动速度为3个单位/秒,点Q从C出发向点B运动,速度为1个单位/秒,P、Q同时出发,点Q到点B时两点同时停止运动.(1)点P在线段AC上运动,过P作DP⊥PQ交边AB于D,t=2时,求$\frac{PD}{PQ}$的值;
(2)运动t秒后,∠BPQ=90°,求此时t的值;
(3)t=$\frac{100}{23}$时,AQ=QP.

分析 (1)如图1中作PE⊥AB于E,PF⊥BC于F,求出PE、PF,由△PED∽△PFQ得$\frac{PD}{PQ}=\frac{PE}{PF}$,由此即可解决.
(2)如图2中作PE⊥AB于E,由△PEB∽△BPQ,得$\frac{PE}{PB}=\frac{PB}{BQ}$,由此即可解决问题.
(3)如图3中作QF⊥AC于F,根据AQ=QP利用勾股定理列出方程即可.
解答 解;(1)如图1中,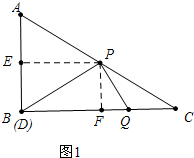 作PE⊥AB于E,PF⊥BC于F,
作PE⊥AB于E,PF⊥BC于F,
∵t=2,
∴AP=6,CQ=2,
∵PE∥BC,
∴$\frac{PA}{AC}=\frac{PE}{BC}=\frac{AE}{AB}$,
∴$\frac{6}{10}=\frac{PE}{8}=\frac{AE}{6}$,
∴PE=4.8,AE=3.6,BE=2.4,
∵∠PEB=∠EBF=∠PFB=90°,
∴四边形EBFP是矩形,
∴PF=BE=2.4,
∵∠EPF=∠QPD=90°,
∴∠EPD=∠FPQ,
∴△PED∽△PFQ,
∴$\frac{PD}{PQ}=\frac{PE}{PF}$=$\frac{4.8}{2.4}$=2.
(2)如图2中,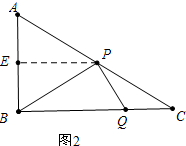 作PE⊥AB于E,
作PE⊥AB于E,
∵PE∥BC,
∴$\frac{PE}{BC}=\frac{AP}{AC}=\frac{AE}{AB}$,
∴PE=$\frac{12}{5}t$,AE=$\frac{9}{5}t$,EB=6-$\frac{9}{5}t$,
∵∠EPB=∠PBQ,∠PEB=∠BPQ=90°,
∴△PEB∽△BPQ,
∴$\frac{PE}{PB}=\frac{PB}{BQ}$,
∴$\frac{12}{5}t•(8-t)=(\frac{12}{5}t)^{2}+(6-\frac{9}{5}t)^{2}$,
∴t=2或$\frac{30}{19}$.
(3)如图3中作QF⊥AC于F,
∵∠QCF=∠ACB,∠QFC=∠ABC,
∴△QFC∽△ABC,
∴$\frac{QF}{AB}=\frac{QC}{AC}$,
∴QF=$\frac{3}{5}$t,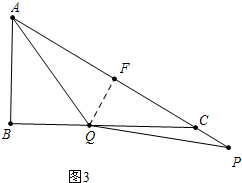
∵AQ=QP,
∴AF=FP=$\frac{3}{2}t$,
∴62+(8-t)2=($\frac{3}{5}$t)2+($\frac{3}{2}$t)2,
整理得:161t2+1600t-10000=0,
解得t=$\frac{100}{23}$(或-$\frac{100}{7}$舍弃).
故答案为$\frac{100}{23}$.
点评 本题考查相似三角形的判定和性质、勾股定理、等腰三角形的性质,添加辅助线构造相似三角形是解决问题的关键,属于中考常考题型.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案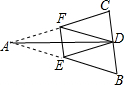 如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )
如图,在△ABC中,AB=AC,点D为BC边的中点,将△ABC沿EF折叠,点A与点D重合,若DE=$\sqrt{10}$,EF=2,则△ABC的面积为( )| A. | 2$\sqrt{10}$ | B. | 4$\sqrt{10}$ | C. | 12 | D. | 24 |
 如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )
如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点Q的坐标为(0,2).点P(x,0)在边AB上运动,若过点Q、P的直线将矩形ABCD的周长分成2:1两部分,则x的值为( )| A. | $\frac{1}{2}$或$-\frac{1}{2}$ | B. | $\frac{1}{3}$或$-\frac{1}{3}$ | C. | $\frac{3}{4}$或$-\frac{3}{4}$ | D. | $\frac{2}{3}$或$-\frac{2}{3}$ |
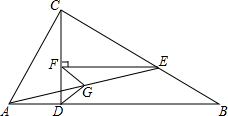 己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.
己知:如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,E是CB上一点,且CE=AC,EF⊥CD,垂足为F.