题目内容
2.已知点A、B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a、b(a>0,b>O).若直线AB为一次函数y=kx+m的图象,则当$\frac{b}{a}$是整数时,满足条件的整数k的值共有2个.分析 根据题意,可以设A(a,a),B(b,8b),据此列出关于a、b的方程组,然后通过解方程组知:(a-b)k=a-8b;从而用$\frac{b}{a}$表示出k;再利用换元法(设$\frac{b}{a}$=t)以及整数的定义求得k值.
解答 解:∵点A,B分别在一次函数y=x与y=8x的图象上,
∴设A(a,a),B(b,8b),则有$\left\{\begin{array}{l}{ak+m=a}\\{bk+m=8b}\end{array}\right.$,
消去m得:(a-b)k=a-8b,
∵当a=b时,a=b=0与题意不符合,
∴a≠b,且k=$\frac{a-8b}{a-b}$=$\frac{1-\frac{8b}{a}}{1-\frac{b}{a}}$;
设$\frac{b}{a}$=t,则
k=$\frac{1-8t}{1-t}$=$\frac{8t-1}{t-1}$=$\frac{8(t-1)+7}{t-1}$,即k=8+$\frac{7}{t-1}$;
∵$\frac{b}{a}$是整数,a>0,b>0,t-1≠0,
∴t是整数,且t>0,t≠1;
又∵k为整数,
∴t-1=7或t-1=1,
∴t=8或t=2,
∴k=9或k=15.
故答案为2.
点评 本题考查了一次函数图象上点的坐标特征以及待定系数法求一次函数解析式的知识,解得该题时,需要讨论a与b的数量关系,以防出现增根.

练习册系列答案
相关题目
14. 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
 如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )
如图,在⊙O上有顶点C和动点P,位于直径AB的两侧,过点C作CP的垂线与PB的延长线交于点Q.已知⊙O的直径为10,tan∠ABC=$\frac{4}{3}$,则CQ最大值为( )| A. | 5 | B. | $\frac{15}{2}$ | C. | $\frac{25}{4}$ | D. | $\frac{20}{3}$ |
11.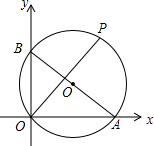 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
 如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )
如图,已知A、B两点坐标分别为(8,0)、(0,6),P是△AOB外接圆上的一点,且∠AOP=45°,则点P的坐标为( )| A. | (8,6) | B. | (7,7) | C. | (7$\sqrt{2}$,7$\sqrt{2}$) | D. | (5$\sqrt{2}$,5$\sqrt{2}$) |
12.如果10b=n,那么称b为n的劳格数,记为b=d (n),由定义可知:10b=n与b=d (n)所表示的是b、n两个量之间的同一关系.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
(1)根据劳格数的定义,填空:d(10)=1,d(10-2)=-2;
劳格数有如下运算性质:
若m、n为正数,则d(mn)=d(m)+d(n),d($\frac{m}{n}$)=d(m)-d(n).
根据运算性质,填空:$\frac{d({a}^{3})}{d(a)}$=3(a为正数).
(2)下表中与数x对应的劳格数d (x)有且只有两个是错误的,请找出错误的劳格数,说明理由并改正.
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d(x) | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |

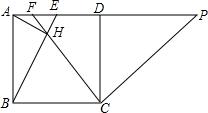 如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$.
如图,在正方形ABCD中,E为AD中点,AH⊥BE于点H,连接CH并延长交AD于点F,CP⊥CF交AD的延长线于点P,若EF=1,则DP的长为$\frac{16}{3}$.