6. 如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
 如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高为8cm,底面周长为30cm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )| A. | 15cm | B. | 17cm | C. | 18cm | D. | 30cm |
3.下列各组数中,能够构成直角形三边的是( )
| A. | 1,$\sqrt{2}$,$\sqrt{3}$ | B. | 3,4,6 | C. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ | D. | $\sqrt{6}$,$\sqrt{8}$,$\sqrt{10}$ |
2.下列各式与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{18}$ | C. | $\sqrt{12}$ | D. | $\sqrt{6}$ |
1.读取表格中的信息,解决问题:
(1)计算:a1+b1+c1=3$\sqrt{2}$+3$\sqrt{3}$+3;
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
0 281033 281041 281047 281051 281057 281059 281063 281069 281071 281077 281083 281087 281089 281093 281099 281101 281107 281111 281113 281117 281119 281123 281125 281127 281128 281129 281131 281132 281133 281135 281137 281141 281143 281147 281149 281153 281159 281161 281167 281171 281173 281177 281183 281189 281191 281197 281201 281203 281209 281213 281219 281227 366461
| n=1 | a1=$\sqrt{2}$+2$\sqrt{3}$ | b1=$\sqrt{3}$+2 | c1=1+2$\sqrt{2}$ |
| n=2 | a2=b1+2c1 | b2=c1+2a1 | c2=a1+2b1 |
| n=3 | a3=b2+2c2 | b3=c2+2a2 | c3=a2+2b2 |
| … | … | … | … |
(2)满足$\frac{{{a_n}+{b_n}+{c_n}}}{{\sqrt{3}+\sqrt{2}}}≥81(\sqrt{3}-\sqrt{2}+1)$的n可以取得的最小正整数是4.
 如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.
如图,AC=AD,线段AB经过线段CD的中点E,求证:BC=BD.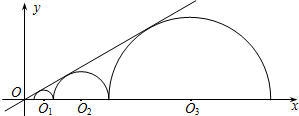 如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015.
如图,圆心都在x轴正半轴上的半圆O1、半圆O2、…、半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1、半圆O2、…、半圆On的半径分别是r1、r2、…、rn,则当r1=1时,r2016=32015. 如图所示的图形是由7个完全相同的小正方体组成的立体图形,则下面四个平面图形中,从三个方向看不能得到的图形是( )
如图所示的图形是由7个完全相同的小正方体组成的立体图形,则下面四个平面图形中,从三个方向看不能得到的图形是( )



