题目内容
19.课本指出:公认的真命题称为基本事实,除了基本事实外,其他的真命题(如推论、定理等)的正确性都需要借助基本事实,通过推理的方法证实.例如:我们学过三角形全等的基本事实有三个,即:“SSS”、“SAS”、“ASA”,请你完成以下问题:(1)叙述三角形全等的判定方法中的推论AAS:如果两个三角形的两个角及其中一个角的对边对应相等,那么这两个三角形全等.
(2)小红同学对这个推论的正确性进行了证明,她画出了△ABC和△DEF,并写出了如下不完整的已知和求证.
(3)按小红的想法写出证明.
证明:

分析 (1)根据全等三角形的判定定理即可得到结论;
(2)根据题意即可得到结论;
(3)在△ABC与△DEF中,∠B=∠E,∠A=∠D,证得∠C=∠F,根据全等三角形的判定定理即可得到结论.
解答 解:(1)两个角;角的对边;
故答案为:两个角,角的对边;
(2)∠D;BC;
(3)在△ABC与△DEF中,∠B=∠E,∠A=∠D,
∴∠B+∠A=∠E+∠D,
又∵∠A+∠B+∠C=180°,∠D+∠E+∠F=180°,
∴∠C=∠F,
在△ABC与△DEF中,$\left\{\begin{array}{l}{∠C=∠F}\\{BC=EF}\\{∠B=∠E}\end{array}\right.$,
∴△ABC≌△DEF(ASA).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
9. 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC.下列比例式正确的是( )
如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC.下列比例式正确的是( )
 如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC.下列比例式正确的是( )
如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC.下列比例式正确的是( )| A. | $\frac{AD}{DB}$=$\frac{CE}{AE}$ | B. | $\frac{AD}{DB}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | D. | $\frac{AD}{AB}$=$\frac{EC}{AE}$ |
8.对于直线、射线、线段,在下列各图中能相交的是( )
| A. |  | B. |  | C. |  | D. |  |
19.不解方程,判别方程2x2-2$\sqrt{2}$x+1=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |

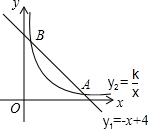 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(a,1)、B(1,b)两点.