Question

7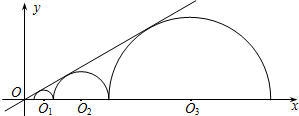．如图，圆心都在x轴正半轴上的半圆O₁、半圆O₂、…、半圆O_n与直线$y=\frac{{\sqrt{3}}}{3}x$相切，设半圆O₁、半圆O₂、…、半圆O_n的半径分别是r₁、r₂、…、r_n，则当r₁=1时，r₂₀₁₆=3²⁰¹⁵．

Answer 1

分析 先求出r₁=1，r₂=3，r₃=9…r_n=3^n-1，根据规律即可解决．

解答 解：设A、B、C是切点，由题意直线y=$\frac{\sqrt{3}}{3}$x与x轴的夹角为30°，
在RT△OO₁A中，∵AO₁=1，∠AOO₁=30°，
∴OO₁=2AO₁=2，
同理：OO₂=2BO₂，OO₃=2CO₃，
∴3+r₂=2r₂，
∴r₂=3，
9+r₃=2r₃，
r₃=9，
∴r₁=1，r₂=3，r₃=9…r_n=3^n-1，
∴r₂₀₁₆=3²⁰¹⁵．
故答案为3²⁰¹⁵．

点评 本题考查圆的切线的性质、直角三角形中30度角的性质、学会从特殊到一般的推理方法，寻找规律是解决问题的关键．