解下列方程:
(1)
+
=
;
(2)
+
+
=0;
(3)(x+1)(x+2)(x+3)(x+4)=120;
(1)
| x2+x+1 |
| x2+1 |
| 2x2+x+2 |
| x2+x+1 |
| 19 |
| 6 |
(2)
| 1 |
| x2+11x-8 |
| 1 |
| x2+2x-8 |
| 1 |
| x2-13x-8 |
(3)(x+1)(x+2)(x+3)(x+4)=120;
 下面所说的“平移”,是指只沿方格的格线(即上下或左右)运动,将图中的任一条线段平移1格称为“1步”.要通过平移,使图中的3条线段首尾相接组成一个三角形,最少需要移动( )
下面所说的“平移”,是指只沿方格的格线(即上下或左右)运动,将图中的任一条线段平移1格称为“1步”.要通过平移,使图中的3条线段首尾相接组成一个三角形,最少需要移动( )| A、7步 | B、8步 | C、9步 | D、10步 |
如图,一条两边平行的纸带的宽度(两平行线间的距离)为8cm,现将纸带折起压平(两条相对的长边应相交),那么重叠部分△ABC面积的最小值为( )


| A、16cm2 |
| B、32cm2 |
| C、64cm2 |
| D、无最小值 |
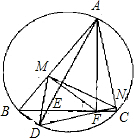 如图,在锐角△ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N是垂足),延长AE交△ABC的外接圆于点D.
如图,在锐角△ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N是垂足),延长AE交△ABC的外接圆于点D. 如图所示,某市自来水公司职工养老保险个人月缴费y(元)随个人工资x(元)的变化情况,则:
如图所示,某市自来水公司职工养老保险个人月缴费y(元)随个人工资x(元)的变化情况,则: