题目内容
方程组
的解是 .
|
考点:高次方程
专题:整体思想
分析:首先把x+y和xy看成一个整体,令A=x+y,b=xy,进而解得A、B的解,最后解得x、y.
解答:解:整理得
,
令A=x+y,b=xy,则
,
从而可解出
;
;
;
.
|
令A=x+y,b=xy,则
|
从而可解出
|
|
|
|
点评:本题主要考查高次方程求解的问题,解决此类问题的关键是把高次方程转变成低次方程进行求解,此类题具有一定的难度,同学们解决时需要细心.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知多项式p1(x)=2x2-5x+1和p2(x)=3x-4,则p1(x)×p2(x)的最简结果为( )
| A、6x3-23x2+23x-4 |
| B、6x3+23x2-23x-4 |
| C、6x3-23x2-23x+4 |
| D、6x3+23x2+23x+4 |
若k=
=
=
(a+b+c≠0),则k的值为( )
| 2a+b |
| c |
| 2c+a |
| b |
| 2b+c |
| a |
| A、1 | B、2 | C、3 | D、非上述答案 |
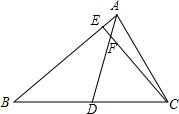 如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )
如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )| A、1:6 | B、1:8 |
| C、1:9 | D、1:10 |
 变与不变将一长方形纸片折出如图所示的图形,其中∠AEB=30°,BG:GH:HC=2:4:1,如果DH=3cm,求AE+EF的长.
变与不变将一长方形纸片折出如图所示的图形,其中∠AEB=30°,BG:GH:HC=2:4:1,如果DH=3cm,求AE+EF的长. 如图所示,某市自来水公司职工养老保险个人月缴费y(元)随个人工资x(元)的变化情况,则:
如图所示,某市自来水公司职工养老保险个人月缴费y(元)随个人工资x(元)的变化情况,则: