题目内容
方程组
的解的个数为 .
|
考点:高次方程
专题:计算题
分析:首先根据(1)(2)式子之间的关系,可以求出xyz=0,然后令x为0,解得y、z的值.
解答:解:由(1)(2)联立得xy+yz+xz=20(4)
而x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)
∴189-3xyz=9(41-20)
∴xyz=0
∴x=0或y=0或z=0.把x=0分别代入式(1)(4)得
,
又由于原方程组是关于x、y、z的对称方程组,故原方程组有6组解.
而x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)
∴189-3xyz=9(41-20)
∴xyz=0
∴x=0或y=0或z=0.把x=0分别代入式(1)(4)得
|
|
又由于原方程组是关于x、y、z的对称方程组,故原方程组有6组解.
点评:本题主要考查高次方程求解的问题,解决此类问题的关键是把高次方程转变成低次方程进行求解,此类题具有一定的难度,同学们解决时需要细心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
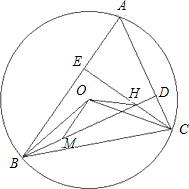 如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.
如图,⊙O为△ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH. 将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于
将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于