题目内容
解下列方程:
(1)
+
=
;
(2)
+
+
=0;
(3)(x+1)(x+2)(x+3)(x+4)=120;
(1)
| x2+x+1 |
| x2+1 |
| 2x2+x+2 |
| x2+x+1 |
| 19 |
| 6 |
(2)
| 1 |
| x2+11x-8 |
| 1 |
| x2+2x-8 |
| 1 |
| x2-13x-8 |
(3)(x+1)(x+2)(x+3)(x+4)=120;
考点:高次方程,换元法解分式方程
专题:计算题,换元法
分析:(1)由于
=
=1+
,此时发现两个分式具备倒数关系,
设y=
,则原方程另一个分式为1+
,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
(2)观察发现方程左边三个分式的分母都是关于未知数x的二次三项式,且二次项都是x2,常数项都是-8,设y=x2+2x-8,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
(3)先运用乘法交换律与结合律将(x+1)与(x+4)相乘,(x+2)与(x+3)相乘,再设x2+5x+4=y,
则原方程化为y2+2y-120=0.用换元法解一元二次方程先求y,再求x.
| 2x2+x+2 |
| x2+x+1 |
| (x2+x+1)+(x2+1) |
| x2+x+1 |
| x2+1 |
| x2+x+1 |
设y=
| x2+x+1 |
| x2+1 |
| 1 |
| y |
(2)观察发现方程左边三个分式的分母都是关于未知数x的二次三项式,且二次项都是x2,常数项都是-8,设y=x2+2x-8,可用换元法转化为关于y的分式方程.先求y,再求x.结果需检验.
(3)先运用乘法交换律与结合律将(x+1)与(x+4)相乘,(x+2)与(x+3)相乘,再设x2+5x+4=y,
则原方程化为y2+2y-120=0.用换元法解一元二次方程先求y,再求x.
解答:解:(1)原方程可变形为
+1+
=
,
+
=
.
令y=
,则原方程可变为y+
=
,
解得y1=
,y2=
.
当y1=
时,
=
,解得x=1;
当y2=
时,
=
,解得x=
.
经检验:x=1或
都是原方程的解.
故原方程的解为x1=1,x2=
,x3=
.
(2)设x2+2x-8=y,则原方程可化为:
+
+
=0,
方程的两边同乘y(y+9x)(y-15x),整理得y2-4xy-45x2=0,
解得y=9x或y=-5x.
当y=9x时,x2+2x-8=9x,x2-7x-8=0,解得x1=8,x2=-1;
当y=-5x时,x2+2x-8=-5x,x2+7x-8=0,解得x3=-8,x4=1.
经检验:x1=8,x2=-1,x3=-8,x4=1都是原方程的解.
故原方程的解为x1=8,x2=-1,x3=-8,x4=1.
(3)[(x+1)(x+4)][(x+2)(x+3)]=120,
(x2+5x+4)(x2+5x+6)=120,
设x2+5x+4=y,则y(y+2)=120,
∴y2+2y-120=0,
解得y=10或y=-12.
当y=10时,x2+5x+4=10,x2+5x-6=0,解得x1=-6,x2=1;
当y=-12时,x2+5x+4=-12,x2+5x+16=0,△=25-64=-39<0,故此方程无实根.
故原方程的解为x1=-6,x2=1.
| x2+x+1 |
| x2+1 |
| x2+1 |
| x2+x+1 |
| 19 |
| 6 |
| x2+x+1 |
| x2+1 |
| x2+1 |
| x2+x+1 |
| 13 |
| 6 |
令y=
| x2+x+1 |
| x2+1 |
| 1 |
| y |
| 13 |
| 6 |
解得y1=
| 3 |
| 2 |
| 2 |
| 3 |
当y1=
| 3 |
| 2 |
| x2+x+1 |
| x2+1 |
| 3 |
| 2 |
当y2=
| 2 |
| 3 |
| x2+x+1 |
| x2+1 |
| 2 |
| 3 |
-3±
| ||
| 2 |
经检验:x=1或
-3±
| ||
| 2 |
故原方程的解为x1=1,x2=
-3+
| ||
| 2 |
3-
| ||
| 2 |
(2)设x2+2x-8=y,则原方程可化为:
| 1 |
| y+9x |
| 1 |
| y |
| 1 |
| y-15x |
方程的两边同乘y(y+9x)(y-15x),整理得y2-4xy-45x2=0,
解得y=9x或y=-5x.
当y=9x时,x2+2x-8=9x,x2-7x-8=0,解得x1=8,x2=-1;
当y=-5x时,x2+2x-8=-5x,x2+7x-8=0,解得x3=-8,x4=1.
经检验:x1=8,x2=-1,x3=-8,x4=1都是原方程的解.
故原方程的解为x1=8,x2=-1,x3=-8,x4=1.
(3)[(x+1)(x+4)][(x+2)(x+3)]=120,
(x2+5x+4)(x2+5x+6)=120,
设x2+5x+4=y,则y(y+2)=120,
∴y2+2y-120=0,
解得y=10或y=-12.
当y=10时,x2+5x+4=10,x2+5x-6=0,解得x1=-6,x2=1;
当y=-12时,x2+5x+4=-12,x2+5x+16=0,△=25-64=-39<0,故此方程无实根.
故原方程的解为x1=-6,x2=1.
点评:本题主要考查高次方程求解的问题,解决此类问题的关键是把高次方程转变成低次方程进行求解,注意运用换元法进行解题,此类题具有一定的难度,同学们解决时需要细心.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
如图,一条两边平行的纸带的宽度(两平行线间的距离)为8cm,现将纸带折起压平(两条相对的长边应相交),那么重叠部分△ABC面积的最小值为( )


| A、16cm2 |
| B、32cm2 |
| C、64cm2 |
| D、无最小值 |
方程|x2-1|=
(x+
)的实根个数为( )
| 1 |
| 10 |
| 9 |
| 10 |
| A、4 | B、3 | C、2 | D、1 |
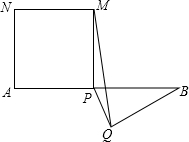 如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于
如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于