题目内容
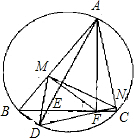 如图,在锐角△ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N是垂足),延长AE交△ABC的外接圆于点D.
如图,在锐角△ABC的BC边上有两点E、F,满足∠BAE=∠CAF,作FM⊥AB,FN⊥AC(M、N是垂足),延长AE交△ABC的外接圆于点D.证明:四边形AMDN与△ABC的面积相等.
考点:相似三角形的判定与性质,四点共圆
专题:证明题
分析:根据FM⊥AB,FN⊥AC,得到A,M,D,N四点共圆,得到MN⊥AD,再用两角对应相等证明两三角形相似,利用相似三角形的性质,相似三角形对应边的比相等证明四边形的面积与三角形的面积相等.
解答: 证明:如图:连接BD,
证明:如图:连接BD,
∵FM⊥AB于点M,FN⊥AC于点N,
∴A,M,F,N四点共圆,
∴∠AMN=∠AFN,
∴∠AMN+∠BAE=∠AFN+∠CAF=90°,
即MN⊥AD,
∴S四边形AMDN=
AD•MN,
∵∠CAF=∠DAB,∠ACF=∠ADB,
∴△AFC∽△ABD,
∴AF:AB=AC:AD,
∴AB•AC=AD•AF,
∵AF是过A、M、F、N四点的圆的直径,
∴
=AF,
∴AF•sin∠ABC=MN,
∴S△ABC=
AB•AC•sin∠BAC=
AD•AF•sin∠BAC=
AD•MN=S四边形AMDN.
∴S△ABC=S四边形AMDN.
 证明:如图:连接BD,
证明:如图:连接BD,∵FM⊥AB于点M,FN⊥AC于点N,
∴A,M,F,N四点共圆,
∴∠AMN=∠AFN,
∴∠AMN+∠BAE=∠AFN+∠CAF=90°,
即MN⊥AD,
∴S四边形AMDN=
| 1 |
| 2 |
∵∠CAF=∠DAB,∠ACF=∠ADB,
∴△AFC∽△ABD,
∴AF:AB=AC:AD,
∴AB•AC=AD•AF,
∵AF是过A、M、F、N四点的圆的直径,
∴
| MN |
| sin∠BAC |
∴AF•sin∠ABC=MN,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABC=S四边形AMDN.
点评:本题考查的是相似三角形的判定与性质,根据两角对应相等可以得到两组相似三角形,利用相似三角形的性质,相似三角形对应边的比相等,得到线段乘积的形式,证明四边形的面积与三角形的面积相等.

练习册系列答案
相关题目
将a千克含盐10%的盐水配制成含盐15%的盐水,需加盐x千克,则由此可列出方程为( )
| A、a(1-10%)=(a+x)(1-15%) |
| B、a×10%=(a+x)×15% |
| C、a×10%+x=a×15% |
| D、a(1-10%)=x(1-15%) |
某工厂去年的生产总值比前年增长了P%,那么,前年的生产总值比去年减少的百分数是( )
| A、P% | ||
B、
| ||
C、
| ||
D、(1+
|
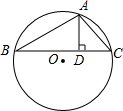 如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=
如图,已知△ABC内接于⊙O,AB+AC=12,AD⊥BC于D,AD=3,设⊙O的半径为y,AB的长为x,用x的代数式表示y,y=
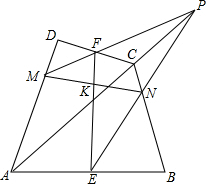 如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.
如图,四边形中ABCD中,E,F分别是AB,CD的中点,P为对角线AC延长线上的任意一点,PF交AD于M,PE交BC于N,EF交MN于K.