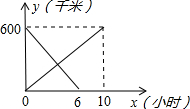
 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
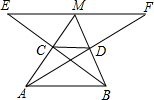 如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )
如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
 如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )
如图,在梯形ABCD中,AB∥CD,AB=a,CD=b,两腰的延长线交于点M,过M作DC的平行线,分别交BC、AD的延长线于点E、F,则EF等于( )A、
| ||
B、
| ||
C、
| ||
D、
|