题目内容
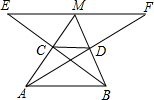如图，在梯形ABCD中，AB∥CD，AB=a，CD=b，两腰的延长线交于点M，过M作DC的平行线，分别交BC、AD的延长线于点E、F，则EF等于（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相似三角形的判定与性质
专题：
分析：易证△MCD∽△MAB，
=
=
，即可求得
的值，易证△BCD∽△EMB，可得
=
，即可求得EM的长，同理可求得FM的长，即可解题．
| MD |
| BM |
| CD |
| AB |
| b |
| a |
| BD |
| BM |
| CD |
| EM |
| BD |
| BM |
解答：解：∵CD∥AB，
∴△MCD∽△MAB，
∴
=
=
，
∴
=1-
=
，
∵EF∥CD，
∴△BCD∽△EMB，
∴
=
=
，
∴EM=
，
同理FM=
，
∴EF=
．
故选 B．
∴△MCD∽△MAB，
∴
| MD |
| BM |
| CD |
| AB |
| b |
| a |
∴
| BD |
| BM |
| MD |
| BM |
| a-b |
| a |
∵EF∥CD，
∴△BCD∽△EMB，
∴
| CD |
| EM |
| BD |
| BM |
| a-b |
| a |
∴EM=
| ab |
| a-b |
同理FM=
| ab |
| a-b |
∴EF=
| 2ab |
| a-b |
故选 B．
点评：本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△MCD∽△MAB和△BCD∽△EMB是解题的关键．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
如图所示，长方形由大小不一的正方形组成，原来的长方形的周长为68cm，那么原来长方形的长为（ ）| A、18cm | B、20cm |
| C、16cm | D、22cm |
下列运算正确的是（ ）
| A、x6÷x2=x3 | ||||||
B、
| ||||||
| C、（x+2y）2=x2+2xy+4y2 | ||||||
D、
|
已知如图，I是△ABC的内心，以内切圆的半径为边长的正方形IDEF、EFHG放置于△ABC内，D、E、H、G都在三角形的边上，则tanC的值是 （ ）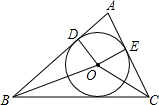
如图所示，⊙O是△ABC的内切圆，切AB、AC于点D、E．
如图，已知AB是⊙O的直径，CD切⊙O于点D，BE切⊙O于点B，交CD于点E，⊙O的半径为a，BC=na，则DE：EC=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|