题目内容
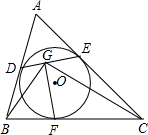 已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF.
已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF.考点:三角形的内切圆与内心
专题:证明题
分析:连接OF,OB,OC,OC,连接DF,EF,证明△DGF∽△OFC,△EGF∽△OFB,即可证明DG•CF=EG•BF.
解答: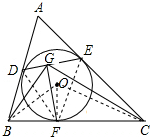 证明:连接OF,OB,OC,OC,连接DF,EF,
证明:连接OF,OB,OC,OC,连接DF,EF,
∵⊙O为△ABC的内切圆,
∴CE=CF,BD=BF,
∴∠FDE=∠COF,而∠DGF=∠OFC=90°,
∴△DGF∽△OFC,同理△EGF∽△OFB,
∴
=
,
=
,
∴OF•GF=GD•CF=GD•CE,
OF•GF=GE•BF=GE•BD,
∴GD•CE=GE•BD,
即DG•CF=EG•BF.
 证明:连接OF,OB,OC,OC,连接DF,EF,
证明:连接OF,OB,OC,OC,连接DF,EF,∵⊙O为△ABC的内切圆,
∴CE=CF,BD=BF,
∴∠FDE=∠COF,而∠DGF=∠OFC=90°,
∴△DGF∽△OFC,同理△EGF∽△OFB,
∴
| DG |
| OF |
| GF |
| CF |
| GE |
| OF |
| GF |
| BF |
∴OF•GF=GD•CF=GD•CE,
OF•GF=GE•BF=GE•BD,
∴GD•CE=GE•BD,
即DG•CF=EG•BF.
点评:本题考查了相似三角形的判定与性质及三角形内切圆与内心,难度适中,关键是巧妙作出辅助线.

练习册系列答案
相关题目
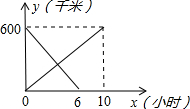 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
“六一”期间,某商店将单价标为130元的书包按8折出售可获利30%,该书包每个的进价是( )
| A、65元 | B、80元 |
| C、100元 | D、104元 |
 已知线段a、b(a>b)
已知线段a、b(a>b)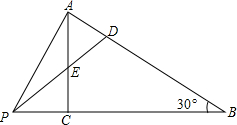 如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.
如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.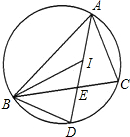 如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.
如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E,求证:ID=BD.