题目内容
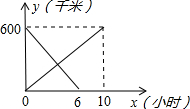 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,两车距甲地的距离y千米与行驶时间x小时之间的函数图象如图所示,则下列说法中错误的是( )| A、客车比出租车晚4小时到达目的地 |
| B、客车速度为60千米/时,出租车速度为100千米/时 |
| C、两车出发后3.75小时相遇 |
| D、两车相遇时客车距乙地还有225千米 |
考点:一次函数的应用
专题:
分析:观察图形可发现客车出租车行驶路程均为600千米,客车行驶了10小时,出租车行驶了6小时,即可求得客车和出租车行驶时间和速度;
易求得直线AC和直线OD的解析式,即可求得交点横坐标x,即可求得相遇时间,和客车行驶距离,即可解题.
易求得直线AC和直线OD的解析式,即可求得交点横坐标x,即可求得相遇时间,和客车行驶距离,即可解题.
解答:解:(1)∵客车行驶了10小时,出租车行驶了6小时,∴客车比出租车晚4小时到达目的地,故A正确;
(2)∵客车行驶了10小时,出租车行驶了6小时,∴客车速度为60千米/时,出租车速度为100千米/时,故B正确;
(3)∵设出租车行驶时间为x,距离目的地距离为y,
则y=-100x+600,
设客车行驶时间为x,距离目的地距离为y,
则y=60x;
当两车相遇时即60x=-100x+600时,x=3.75h,故C正确;
∵3.75小时客车行驶了60×3.75=225千米,
∴距离乙地600-225=375千米,故D错误;
故选 D.
(2)∵客车行驶了10小时,出租车行驶了6小时,∴客车速度为60千米/时,出租车速度为100千米/时,故B正确;

(3)∵设出租车行驶时间为x,距离目的地距离为y,
则y=-100x+600,
设客车行驶时间为x,距离目的地距离为y,
则y=60x;
当两车相遇时即60x=-100x+600时,x=3.75h,故C正确;
∵3.75小时客车行驶了60×3.75=225千米,
∴距离乙地600-225=375千米,故D错误;
故选 D.
点评:本题考查了一次函数解析式的求解,考查了一次函数交点的求解,本题中正确求得一次函数解析式是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
等边三角形可以看作是自身的一个旋转图形,如果用它的两条角平分线的交点作为旋转中心,那么旋转角的度数是( )
| A、60° | B、120° |
| C、150° | D、180° |
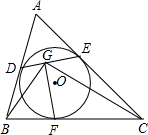 已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF.
已知:⊙O是△ABC的内切圆,D,E,F是切点,FG⊥DE,垂足为G.求证:DG•CF=EG•BF.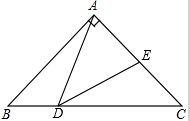 已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为
已知,如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,D是BC边上的一个动点(不与B、C重合)∠ADE=45°,当△ADE是等腰三角形时,EC的长度为 如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证;
如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证; 如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6
如图,在梯形ABCD中,AD∥BC,△AOD的面积与△BOC的面积之比为1:9,△AOB的面积为6