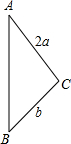
 如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )
如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )| A、2πa2 |
| B、πab |
| C、3πa2+πab |
| D、πa(2a+b) |
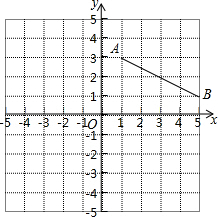 如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( )
如图,线段AB放在边长为1个单位的小正方形网格中,点A、B均落在格点上,先将线段AB绕点O逆时针旋转90°得到线段A1B1,再将线段AB向下平移3个单位得到线段A2B2,线段AB,A1B1,A2B2的中点构成三角形面积为( )A、
| ||
| B、15 | ||
| C、3 | ||
D、
|
 如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )
如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )| A、15° | B、60° |
| C、45° | D、75° |
 如图,△ABC的内心为点I,外心为点O,且∠BIC=115°,求∠BOC的度数.
如图,△ABC的内心为点I,外心为点O,且∠BIC=115°,求∠BOC的度数.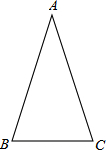 如图,在△ABC中,AB=AC,∠ABC=72°.
如图,在△ABC中,AB=AC,∠ABC=72°. 在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC.
在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC. 如图所示,AB,AC为⊙O的两弦,D为
如图所示,AB,AC为⊙O的两弦,D为
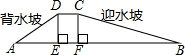 如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE=
如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE=