题目内容
盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是
,写出表示x和y关系的表达式.
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为
,求x和y的值.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是
| 3 |
| 8 |
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为
| 1 |
| 2 |
考点:概率公式
专题:
分析:(1)根据盒中有x枚黑棋和y枚白棋,得出袋中共有(x+y)个棋,再根据概率公式列出关系式即可;
(2)根据概率公式和(1)求出的关系式列出关系式,再与(1)得出的方程联立方程组,求出x,y的值即可.
(2)根据概率公式和(1)求出的关系式列出关系式,再与(1)得出的方程联立方程组,求出x,y的值即可.
解答:解:(1)∵盒中有x枚黑棋和y枚白棋,
∴袋中共有(x+y)个棋,
∵黑棋的概率是
,
∴可得关系式
=
;
(2)如果往口袋中再放进10个黑球,则取得黑棋的概率变为
,又可得
=
;
联立求解可得x=15,y=25.
∴袋中共有(x+y)个棋,
∵黑棋的概率是
| 3 |
| 8 |
∴可得关系式
| x |
| x+y |
| 3 |
| 8 |
(2)如果往口袋中再放进10个黑球,则取得黑棋的概率变为
| 1 |
| 2 |
| x+10 |
| x+y+10 |
| 1 |
| 2 |
联立求解可得x=15,y=25.
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
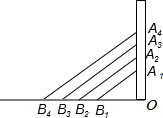 斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )
斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )| A、60m,40m |
| B、60m,30m |
| C、40m,20m |
| D、40m,10m |
 如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )| A、14 | B、18 | C、24 | D、48 |
 如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点R,试问∠R与∠A有什么关系?证明你的结论.
如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点R,试问∠R与∠A有什么关系?证明你的结论. 在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC.
在△ABC中,∠A=60°,以BC为直径作圆O交AC于点D,交AB于点E,连接DE,BD,CE.试证明:△ADE∽△ABC.