题目内容
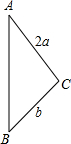 如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )
如图所示,在△ABC中,∠A=30°,AC=2a,BC=b,以直线AB为轴旋转一周,得到一个几何体,这个几何体的全面积是( )| A、2πa2 |
| B、πab |
| C、3πa2+πab |
| D、πa(2a+b) |
考点:圆锥的计算,点、线、面、体
专题:计算题
分析:以直线AB为轴旋转一周,得到一个由两个底面相同的圆锥组成的几何体,作CD⊥AB,则CD为几何体的底面圆的半径,如图,根据含30度的直角三角形三边的关系计算出CD=a,然后利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算两个圆锥的侧面积的和即可.
解答:解:作CD⊥AB,则CD为几何体的底面圆的半径,如图,
在Rt△ADC中,∵∠CAD=30°,
∴CD=
AC=
•2a=a,
∴以AC为母线的圆锥的侧面积=
•2π•a•2a=2πa2;
以BC为母线的圆锥的侧面积=
•2π•a•b=2πab,
∴这个几何体的全面积=2πa2+2πab=aα(2a+b).
故选D.

在Rt△ADC中,∵∠CAD=30°,
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴以AC为母线的圆锥的侧面积=
| 1 |
| 2 |
以BC为母线的圆锥的侧面积=
| 1 |
| 2 |
∴这个几何体的全面积=2πa2+2πab=aα(2a+b).
故选D.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )
如图,Rt△ABC中,AC=8,BC=6,∠ACB=90°,分别以AB、BC、AC为直径作三个半圆,那么阴影部分的面积为( )| A、14 | B、18 | C、24 | D、48 |
 已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形.
已知:如图,在矩形ABCD中,对角线AC与BD相交于点O,点M,P,N,Q分别在AO,BO,CO,DC上,且AM=BP=CN=DQ.求证:四边形MPNQ是矩形. 如图所示,从∠1,∠2,∠3,∠4,∠A,∠C,∠ABC,∠ADC中,找出所有的内错角和同旁内角.
如图所示,从∠1,∠2,∠3,∠4,∠A,∠C,∠ABC,∠ADC中,找出所有的内错角和同旁内角. 如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点R,试问∠R与∠A有什么关系?证明你的结论.
如图,在△ABC中,∠ABC的平分线与△ABC的外角∠ACD的平分线交于点R,试问∠R与∠A有什么关系?证明你的结论. 如图所示,AB,AC为⊙O的两弦,D为
如图所示,AB,AC为⊙O的两弦,D为
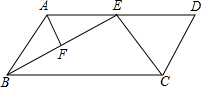 如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.
如图,AB∥CD,BC∥AD,BE、CE分别是∠ABC、∠BCD的平分线,F是BE的中点.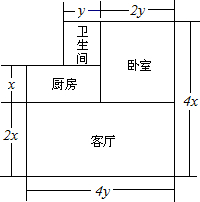 已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)
已知房屋的高度为h m,现老板娘在客厅和卧室的墙壁上贴壁纸,那么至少需要多少平方米的壁纸?如果某种壁纸的价格是b元/m2,那么购买所需壁纸至少需要多少元?(计算时不扣除门,窗所占的面积)