题目内容
如图，△ABC的内心为点I，外心为点O，且∠BIC=115°，求∠BOC的度数．考点：三角形的内切圆与内心,三角形的外接圆与外心
专题：
分析：如图，证明∠ABI=∠CBI（设为α），∠ACI=∠BCI（设为β）；求出α+β=65°，进而求出∠A即可解决问题．
解答：
解：如图，∵△ABC的内心为点I，
∴∠ABI=∠CBI（设为α），∠ACI=∠BCI（设为β），
∵∠BIC=115°，
∴α+β=180°-115°=65°，
∴∠A=180°-2（α+β）=180°-130°=50°，
∴∠BOC=2∠A=100°．
解：如图，∵△ABC的内心为点I，∴∠ABI=∠CBI（设为α），∠ACI=∠BCI（设为β），
∵∠BIC=115°，
∴α+β=180°-115°=65°，
∴∠A=180°-2（α+β）=180°-130°=50°，
∴∠BOC=2∠A=100°．
点评：该题主要考查了三角形内切圆的性质及其应用问题；解题的关键是灵活运用有关定理来分析、解答；对综合的分析问题、解决问题的能力提出了一定的要求．
练习册系列答案
相关题目
如图，在等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．求证：△APQ是等边三角形．
如图，线段AB放在边长为1个单位的小正方形网格中，点A、B均落在格点上，先将线段AB绕点O逆时针旋转90°得到线段A1B1，再将线段AB向下平移3个单位得到线段A2B2，线段AB，A1B1，A2B2的中点构成三角形面积为（ ）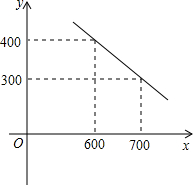
某公司试销一种成本单价为500元/间的新产品，规定试销时的销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系．