题目内容
8．
已知，如图，四边形ABCD，两组对边延长后交E、F，对角线BD∥EF，AC的延长线交EF于G，求证：EG=GF．
分析 过C作EF的平行线分别交AE、AF于M、N，根据平行线分线段成比例定理得到$\frac{BM}{BE}$=$\frac{DN}{DF}$，$\frac{MC}{EF}$=$\frac{BM}{BE}$，$\frac{CN}{EF}$=$\frac{DN}{DF}$，得到MC=NC，证明结论．
解答 证明：
过C作EF的平行线分别交AE、AF于M、N，
∵BD∥EF，
∴MN∥BD，
∴BD∥EF∥MN，
∴$\frac{BM}{BE}$=$\frac{DN}{DF}$，
∵$\frac{MC}{EF}$=$\frac{BM}{BE}$，$\frac{CN}{EF}$=$\frac{DN}{DF}$，
∴MC=NC，
∵$\frac{MC}{EB}$=$\frac{AC}{AG}$=$\frac{NC}{GF}$，
∴EG=GF．
点评 本题考查的是平行线分线段成比例定理，正确作出辅助线、灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
相关题目
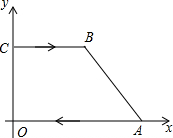四边形ABCD在坐标系中的坐标为A（8，0），B（6，4），C（0，4），O（0，0），P点在CB上从C点向B点运动，运动速度为每秒2个单位；Q点在AO上从A点向O点运动，运动速度为每秒3个单位，P点和Q点同时运动，其中一点达到终点另一点随即停止运动，设运动时间为t秒
如图，在?ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，求BE的长．
如图所示，等腰梯形ABCD中，已知AD∥BC，对角线AC⊥BD，高h=8cm，求它的中位线长．