题目内容
18. 如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长.
如图所示,等腰梯形ABCD中,已知AD∥BC,对角线AC⊥BD,高h=8cm,求它的中位线长.
分析 过点D作DE∥AC交BC的延长线交于点E,DF⊥BC于F,根据平行四边形的性质和等腰梯形的性质得到BD=DE,根据直角三角形的性质得到BE=2DF,根据梯形中位线定理得到答案.
解答 解:过点D作DE∥AC交BC的延长线交于点E,DF⊥BC于F,
∵AD∥BC,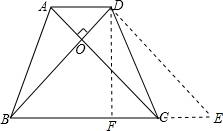
∴四边形ACED是平行四边形,
∴CE=AD,AC=DE,
∵四边形ABCD是等腰梯形,
∴AC=BD,又AC=DE,
∴BD=DE,
∵DE∥AC,AC⊥BD,
∴∠BDE=90°,
∴BE=2DF=16cm,
∵BE=BC+CE=BC+AD,
∴梯形的中位线=$\frac{1}{2}$(BC+AD)=8cm.
点评 本题考查的是等腰梯形的性质、梯形中位线定理、直角三角形的性质,掌握梯形的中位线平行于两底并且等于两底和的一半是解题的关键.

练习册系列答案
相关题目
 已知,如图,四边形ABCD,两组对边延长后交E、F,对角线BD∥EF,AC的延长线交EF于G,求证:EG=GF.
已知,如图,四边形ABCD,两组对边延长后交E、F,对角线BD∥EF,AC的延长线交EF于G,求证:EG=GF.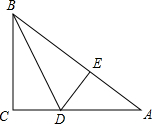 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.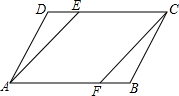 如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF.
如图,在平行四边形ABCD中,BF=DE,求证:∠BAE=∠DCF.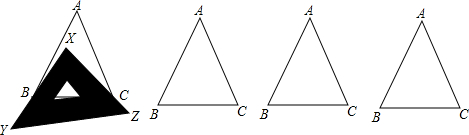
 如图,从A路口到B路口有①、②、③三条路线可走,人们一般情况下选择走②号路线,用几何知识解释其道理应是两点之间,线段最短.
如图,从A路口到B路口有①、②、③三条路线可走,人们一般情况下选择走②号路线,用几何知识解释其道理应是两点之间,线段最短.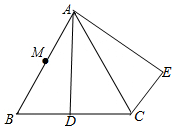 如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD绕点A逆时针旋转到△ACE的位置.