题目内容
19.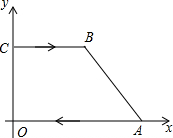 四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒
四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒(1)当t为何值时四边形ABPQ为平行四边形?
(2)当t为何值时,△AQP是以AQ为底边的等腰三角形?
分析 (1)由题意得:CP=2t,AQ=3t,则PB=6-2t,根据平行四边形的判定可得PB=AQ时,四边形ABPQ为平行四边形,因此6-2t=3t,再解即可.
(2过P作PD⊥AO,过Q作QF⊥BC,根据等腰三角形的性质可得DQ=AD=$\frac{1}{2}$QA,由题意得AQ=3t,CP=2t,则DQ=1.5t,QO=8-3t,FP=2t-(8-3t)=5t-8,根据题意可得方程5t-8=1.5t,再解即可.
解答 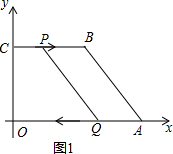 解:(1)如图1:由题意得:CP=2t,AQ=3t,则PB=6-2t,
解:(1)如图1:由题意得:CP=2t,AQ=3t,则PB=6-2t,
当PB=AQ时,四边形ABPQ为平行四边形,
故6-2t=3t,
解得:t=$\frac{6}{5}$,
答:t为$\frac{6}{5}$四边形ABPQ为平行四边形;
(2)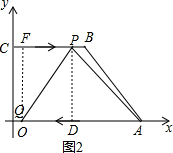 过P作PD⊥AO,过Q作QF⊥BC,
过P作PD⊥AO,过Q作QF⊥BC,
∵△AQP是以AQ为底边的等腰三角形,
∴DQ=AD=$\frac{1}{2}$QA,
∵AQ=3t,
∴DQ=1.5t,QO=8-3t,
∵CP=2t,
∴FP=2t-(8-3t)=5t-8,
∴5t-8=1.5t,
解得:t=$\frac{16}{7}$.
点评 此题主要考查了平行四边形的判定,以及等腰三角形的性质,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
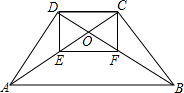 已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形.
已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形. 已知,如图,四边形ABCD,两组对边延长后交E、F,对角线BD∥EF,AC的延长线交EF于G,求证:EG=GF.
已知,如图,四边形ABCD,两组对边延长后交E、F,对角线BD∥EF,AC的延长线交EF于G,求证:EG=GF.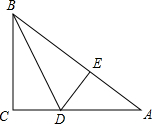 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.