题目内容
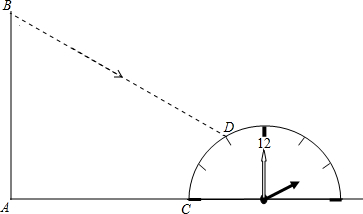
5. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
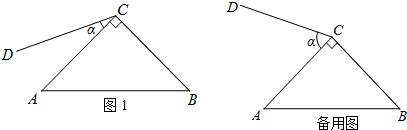
分析 首先过A作AE∥NM,然后判定AE∥GH,根据平行线的性质可得∠3=∠1,再计算出∠4的度数,再根据平行线的性质可得答案.
解答 解:过点A作AE∥NM,
∵NM∥GH,
∴AE∥GH,
∴∠3=∠1=42°32′,
∵∠BAC=60°,
∴∠4=60°-42°32′=17°28′,
∵NM∥AE,
∴∠2=∠4=17°28′,
故选A.
点评 此题主要考查了平行线的判定与性质,关键是掌握两直线平行,内错角相等,此题难度不大.

练习册系列答案
相关题目
16.如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2,那么tanα=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
20.已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线$y=\frac{5}{x}$上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
14. 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |