题目内容
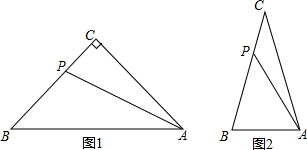
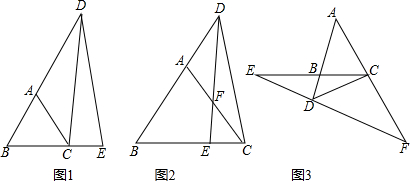
10.在等腰三角形ABC中,AC=BC,点P为BC边上一点(不与B、C重合),连接PA,以P为旋转中心,将线段PA顺时针旋转,旋转角与∠C相等,得到线段PD,连接DB.(1)当∠C=90°时,请你在图1中补全图形,并直接写出∠DBA的度数;
(2)如图2,若∠C=α,求∠DBA的度数(用含α的代数式表示);
(3)连接AD,若∠C=30°,AC=2,∠APC=135°,请写出求AD长的思路.(可以不写出计算结果)
分析 (1)依题意画出图形,如图1所示,先判断出∠BPD=∠EPA,从而得出△PDB≌△PAE,简单计算即可;
(2)先判断出∠CBA=∠CAB,∠BPD=∠EPA,从而得出△PDB≌△PAE,简单代换即可;
(3)先求出BH=2-$\sqrt{3}$,再根据勾股定理得,AB=2$\sqrt{2-\sqrt{3}}$,然后判断出△PAD∽△CAB,从而求出AD.
解答 解:(1)依题意补全图形,如图1所示,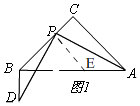
过点P作PE∥AC,
∴∠PEB=∠CAB,
∵AB=BC,
∴∠CBA=∠CAB,
∴∠PEB=∠PBE,
∴PB=PE,
∵∠BPD+∠DPE=∠EPA+∠DPE=90°,
∴∠BPD=∠EPA,
∵PA=PD,
∴△PDB≌△PAE,
∵∠PBA=∠PEB=$\frac{1}{2}$(180°-90°)=45°,
∴∠PBD=∠PEA=180°-∠PEB=135°,
∴∠DBA=∠PBD-∠PBA=90°;
(2)如图2,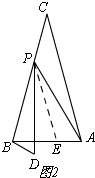
过点P作PE∥AC,
∴∠PEB=∠CAB,
∵AC=BC,
∴∠CBA=∠CAB,
∴∠PEB=∠PBE,
∴PB=PE,
∵∠BPD+∠DPE=∠EPA+∠DPE=α,
∴∠BPD=∠EPA,
∵PA=PD,
∴△PDB≌△PAE,
∵∠PBA=∠PEB=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α,
∴∠PBD=∠PEA=180°-∠PEB=90°+$\frac{1}{2}$α,
∴∠DBA=∠PBD-∠PBA=α;
(3)如图3,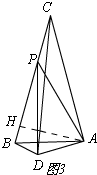
作AH⊥BC,
∵∠ACB=30°,AC=2,
∴AH=1,CH=$\sqrt{3}$,
∴BH=2-$\sqrt{3}$,
根据勾股定理得,AB=$\sqrt{A{H}^{2}+B{H}^{2}}$=2$\sqrt{2-\sqrt{3}}$,
∵∠APC=135°,
∴∠APH=45°,
∴AP=$\sqrt{2}$AH=$\sqrt{2}$,
∵∠APD=∠ACB=30°,AC=BC,AP=DP,
∴△PAD∽△CAB,
∴$\frac{AD}{AB}$=$\frac{AP}{AC}$=$\frac{\sqrt{2}}{2}$,
∴AD=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×2$\sqrt{2-\sqrt{3}}$=$\sqrt{2\sqrt{2}-\sqrt{6}}$.
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,相似三角形的性质和判定,勾股定理,判断△PDB≌△PAE是解本题的关键,也是难点.

 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
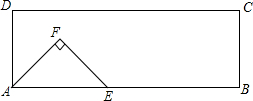 如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).
如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).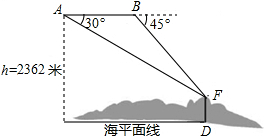 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)