题目内容
13.某广场的旗杆AB旁边有一个半圆的时钟模型,如图所示,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2米,旗杆的底端A到钟面9点刻度C的距离为5米,一天李华同学观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得一米长的标杆的影长1.6米,(1)计算时钟的9点转到11点时的旋转角是多少度?
(2)求旗杆AB的高度.(精确到0.1米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
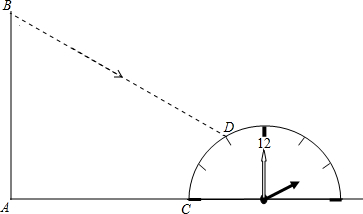
分析 (1)根据钟表的一个大格是30°,从9点转到11点时针转过2个大格,列式计算即可得解.
(2)过点D作DE⊥AC于E,作DF⊥AB于F,设半圆圆心为O,连接OD,解直角三角形求出DE,OE,然后求出DF,再根据同时同地的物高与影长成比例列式求出DF,然后根据AB=AF+DE计算即可得解.
解答 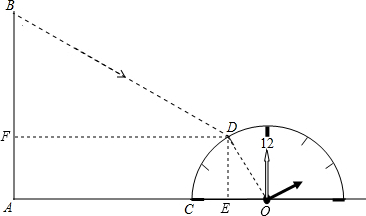 解:(1)从时钟的9点转到11点时时针转过2个大格,
解:(1)从时钟的9点转到11点时时针转过2个大格,
所以,2×30°=60°;
(2)如图,过点D作DE⊥AC于E,作DF⊥AB于F,设半圆圆心为O,连接OD,
∵点D在11点的刻度上,
∴∠COD=60°,
∴DE=OD•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
OE=OD•cos60°=2×$\frac{1}{2}$=1,
∴CE=2-1=1,
∴DF=AE=5+1=6,
∵同时测得一米长的标杆的影长1.6米,
∴$\frac{DF}{BF}$=$\frac{1.6}{1}$,
∴BF=$\frac{6}{1.6}$=$\frac{15}{4}$,
∴AB=BF+DE=($\frac{15}{4}$+$\sqrt{3}$)≈5.5(米).
答:旗杆AB的高度约为5.5米.
点评 本题考查了相似三角形的应用,解直角三角形,作辅助线构造出直角三角形和矩形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.一组数据2,0,-2,1,3的平均数是( )
| A. | 0.8 | B. | 1 | C. | 1.5 | D. | 2 |
5. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
3.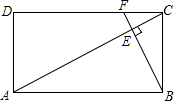 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{25}$ |
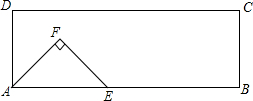 如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).
如图,在矩形ABCD中,AB=6cm,AD=2cm,点E从点A开始,沿射线AB方向平移,在平移过程中,以线段AE为斜边向上作等腰三角形AEF,当EF过点C时,点E停止移动,设点E平移的距离为x(cm),△AEF与矩形ABCD重叠部分的面积为y(cm2).