题目内容
14. 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
分析 根据平行线的性质得到∠ACD=∠A=40°,由角平分线的定义得到∠BCD=2∠ACD=80°,然后根据平行线的性质即可得到结论.
解答 解:∵AB∥CD,
∴∠ACD=∠A=40°,
∵AC平分∠BCD,
∴∠BCD=2∠ACD=80°,
∵AB∥CD,
∴∠B=180°-∠BCD=100°,
故选B.
点评 本题考查了角平分线的定义,平行线的性质,解题的关键是能够发现题目中的一些角的关系,难度不大.

练习册系列答案
相关题目
4.一组数据2,0,-2,1,3的平均数是( )
| A. | 0.8 | B. | 1 | C. | 1.5 | D. | 2 |
5. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
9.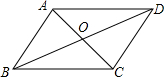 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )| A. | OA=OC,AD∥BC | B. | ∠ABC=∠ADC,AD∥BC | ||
| C. | AB=DC,AD=BC | D. | ∠ABD=∠ADB,∠BAO=∠DCO |
19.关于函数y=$\frac{6}{x}$ 有如下结论:①函数图象一定经过点(-2,-3);②函数图象在第一、三象限;③函数值y随x的增大而增大,这其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.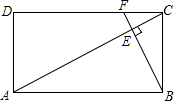 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{25}$ |
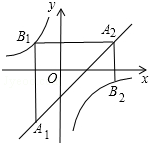 如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.
如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.