题目内容
20.已知点(x1,y1)、(x2,y2)、(x3,y3)在双曲线$y=\frac{5}{x}$上,当x1<0<x2<x3时,y1、y2、y3的大小关系是( )| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y3<y1 |
分析 由反比例系数k=5>0可知,反比例的函数图象过一、三象限,由此可得出y1<0,再结合反比例函数在第一象限单调递减即可得出y2>y3>0,由此即可得出结论.
解答 解:∵k=5>0,
∴反比例函数$y=\frac{5}{x}$图象过一、三象限.
又∵x1<0,
∴y1<0.
当x>0时,反比例函数$y=\frac{5}{x}$单调递减,
又∵0<x2<x3,
∴y2>y3>0.
综上可知:当x1<0<x2<x3时,y1<y3<y2.
故选B.
点评 本题考查了反比例函数的性质,解题的关键是找出y1<0以及y2>y3>0.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的性质确定其图象的单调性,再结合点的横坐标之间的关系即可得出结论.

练习册系列答案
相关题目
10.已知Rt△ABC中,∠C=90°,∠A的正弦是( )
| A. | $\frac{BC}{AB}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BC}{AC}$ | D. | $\frac{AB}{BC}$ |
5. 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
 如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )
如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=42°32′,则∠2的度数( )| A. | 17°28′ | B. | 18°28′ | C. | 27°28′ | D. | 27°32′ |
9.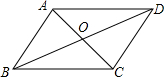 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
 如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )
如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )| A. | OA=OC,AD∥BC | B. | ∠ABC=∠ADC,AD∥BC | ||
| C. | AB=DC,AD=BC | D. | ∠ABD=∠ADB,∠BAO=∠DCO |
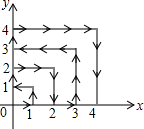 如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
如图,一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(1,0),然后接着按图中箭头所示方向跳动,即(0,0)→(0,1)→(1,1)→(0,1)→…,且每秒跳动一个单位,那么第35秒时跳蚤所在位置的坐标是(0,5).
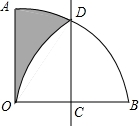 如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)
如图,扇形AOB的圆心角为90°,半径为2,点C为OB中点,点D在$\widehat{AB}$上,将扇形沿直线CD折叠,若点B,O重合,则图中阴影部分的周长为π+2.(结果保留π)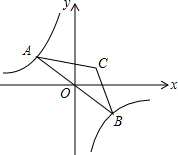 如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.
如图,点A是双曲线y=-$\frac{9}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$上运动,则k的值为3.