题目内容
16.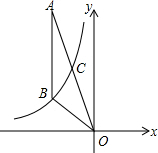 如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).
如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).(1)若点P(-6,m)在反比例函数上,求直线OP的解析式;
(2)求△OAB的面积.
分析 (1)先将点B(-3,2)代入y=$\frac{k}{x}$,利用待定系数法求出反比例函数解析式,再将点P(-6,m)代入反比例函数解析式,求出m的值,得到点P的坐标,然后利用待定系数法即可求出直线OP的解析式;
(2)先由AB∥y轴,点B的坐标为(-3,2),得出A点横坐标为-3,由C是线段OA的中点,根据中点坐标公式得到C点横坐标为-1.5,再将x=-1.5代入y=-$\frac{6}{x}$,求出y的值,得到C点坐标,进而求出A点坐标,然后根据三角形的面积公式即可求解.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(x<0)经过点B(-3,2),
∴k=-3×2=-6,
∴反比例函数解析式为y=-$\frac{6}{x}$,
∵点P(-6,m)在反比例函数上,
∴m=-$\frac{6}{-6}$=1,
∴点P(-6,1).
设直线OP的解析式为y=nx,
则-6n=1,n=-$\frac{1}{6}$,
故直线OP的解析式为y=-$\frac{1}{6}$x;
(2)∵AB∥y轴,点B的坐标为(-3,2),
∴A点横坐标为-3,
∵C是线段OA的中点,
∴C点横坐标为-1.5,
∵当x=-1.5时,y=-$\frac{6}{x}$=-$\frac{6}{-1.5}$=4,
∴C点坐标为(-1.5,4),
∴A点坐标为(-3,8),
∴△OAB的面积=$\frac{1}{2}$×(8-2)×3=9.
点评 此题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数与正比例函数的解析式,反比例函数图象上点的坐标特征,中点坐标公式,三角形的面积.正确求出反比例函数解析式,求得C点坐标,进而求出A点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
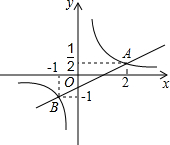 如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点.
如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点. 如图,点P是⊙O外一点,PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,弦AB⊥PF,垂足为D,延长BO交⊙O于点C,连接AC,BF.
如图,点P是⊙O外一点,PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,弦AB⊥PF,垂足为D,延长BO交⊙O于点C,连接AC,BF.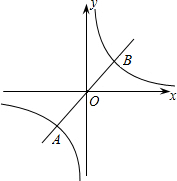 如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,若A点的纵坐标为-2.
如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A、B两点,若A点的纵坐标为-2. 小明一家驾车从家出发到某景区游玩,玩了一段时间后,又驾车回家,图中的折线OABC反映了小明一家离家的距离y(千米)与离家时间x(小时)之间的函数关系图象,请根据图中信息解答下列问题:
小明一家驾车从家出发到某景区游玩,玩了一段时间后,又驾车回家,图中的折线OABC反映了小明一家离家的距离y(千米)与离家时间x(小时)之间的函数关系图象,请根据图中信息解答下列问题: