题目内容
1．已知x-2$\sqrt{xy}$+y=0（x＞0，y＞0），则$\frac{3x-\sqrt{xy}+y}{5x+3\sqrt{xy}-4y}$的值为$\frac{3}{4}$．分析 根据x-2$\sqrt{xy}$+y=0，得（$\sqrt{x}$-$\sqrt{y}$）2=0，可得出x=y，再化简即可．
解答 解：∵x-2$\sqrt{xy}$+y=0（x＞0，y＞0），
∴（$\sqrt{x}$-$\sqrt{y}$）2=0，
∴x=y，
∴原式=$\frac{3x-x+x}{5x+3x-4x}$=$\frac{3x}{4x}$=$\frac{3}{4}$，
故答案为$\frac{3}{4}$．
点评 本题考查了二次根式的化简求值，明确x=（$\sqrt{x}$）2，是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
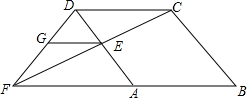如图，已知菱形ABCD中，在AD上任取一点E，连结CE并延长与BA的延长线交于点F，过E作EG∥FB交FD于G，求证：GF=AE．
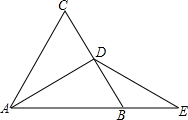如图所示，△ABC是等边三角形，D是BC的中点，延长AB到E，使BE=BD．
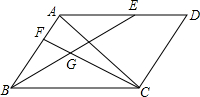如图，平行四边形ABCD中，AB=5，AD=7，AB⊥AC，点E在边AD上，满足$\frac{AE}{AD}$=$\frac{2}{3}$，点F在AB上，满足$\frac{AF}{AB}$=$\frac{2}{5}$，连结BE和CF相交于点G，则线段CG的长度是$\frac{10\sqrt{7}}{7}$．
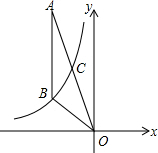如图，反比例函数y=$\frac{k}{x}$（x＜0）经过△OAB的顶点B和线段OA的中点C，AB∥y轴，点B的坐标为（-3，2）．
如图，在?ABCD中，AD=2AB，E，F在直线AB上，CE与AD交于点M，DF与CB交于点N，且AE=AB=BF．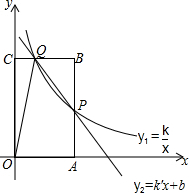
如图，已知矩形OABC在直角坐标系中，点A的坐标是（3，0），点C在y轴的正半轴上，点P是边AB上的一个动点（不与端点A，B重合），设过点P的反比例函数的解析式为y1=$\frac{k}{x}$，且与BC边交于点Q．