题目内容
7. 如图,点P是⊙O外一点,PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,弦AB⊥PF,垂足为D,延长BO交⊙O于点C,连接AC,BF.
如图,点P是⊙O外一点,PA为⊙O的切线,A为切点,直线PO交⊙O于点E、F,弦AB⊥PF,垂足为D,延长BO交⊙O于点C,连接AC,BF.(1)求证:PB与⊙O相切;
(2)若AC=12,tan∠F=$\frac{1}{2}$,求⊙O的直径.
分析 (1)证明:连接OA,由弦AB⊥PF,AD=BD,得到PA=PB,根据三角形全等得到∠PAO=∠PBO.由于PA为⊙O的切线,得到∠PAO=90°,即可得到结果;
(2)根据三角形的中位线的性质得到OD=$\frac{1}{2}$AC=6,由tan∠F=$\frac{1}{2}$,设BD=x,则DF=2x,OB=OF=DF-OD=6,在Rt△BOD中,由勾股定理列方程即可得到结论.
解答 (1)证明:连接OA,
∵弦AB⊥PF,AD=BD,
∴PA=PB,
在△APO和△BPO中,
$\left\{\begin{array}{l}{AD=BD}\\{PA=BA}\\{PO=PO}\end{array}\right.$,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO.
∵PA为⊙O的切线,
∴∠PAO=90°.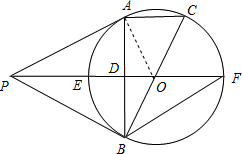
∴∠PBO=90°
∴PB与⊙O相切;
(2)∵AD=BD,BO=CO,
∴OD=$\frac{1}{2}$AC=6,
∵tan∠F=$\frac{1}{2}$,
∴设BD=x,则DF=2x,AB=2x,
在Rt△BOD中,OB2=BD2+OD2,
∴(2x-6)2=x2+62,
解得:x=8,
∴OB=10
∴⊙O的直径是2BO=2×10=20.
点评 此题考查了切线的判定与性质,全等三角形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
18.计算:(-a)3•a2正确的结果是( )
| A. | -a5 | B. | a5 | C. | -a6 | D. | a6 |
2.若点A(-2,a)、B(-1,b)、C(3,c)都在二次函数y=mx2(m<0)图象上,则a、b、c的大小关系是( )
| A. | c<a<b | B. | b<a<c | C. | a<b<c | D. | c<b<a |
17.山西西龙池抽水蓄能电站是国家在本地区有史以来最大的生产性项目,该蓄能在电站装有四台300MW坚轴单级混流可逆式水泵水轮发电组,则单独一台水电机2h发电的电能是( )
| A. | 2.16×1012J | B. | 21.6×1014J | C. | 0.216×1013J | D. | 2.16×1011J |
 如图所示,矩形ABCD沿EF折叠,若∠DEF=72°,则∠AEG的度数为36°.
如图所示,矩形ABCD沿EF折叠,若∠DEF=72°,则∠AEG的度数为36°.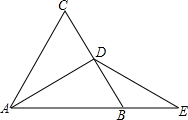 如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.
如图所示,△ABC是等边三角形,D是BC的中点,延长AB到E,使BE=BD.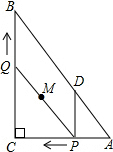 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t>0).
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P,Q分别从点A,C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t秒(t>0).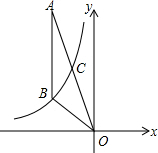 如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).
如图,反比例函数y=$\frac{k}{x}$(x<0)经过△OAB的顶点B和线段OA的中点C,AB∥y轴,点B的坐标为(-3,2).